
| A. | 2 | B. | 3 | C. | 4 | D. | 随t的变化而变化 |
分析 作出函数f(x)的大致图象,分析关于f(x)这一整体的二次方程根的情况,依据根的情况分类讨论.
解答 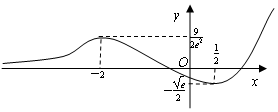 解:∵f′(x)=(x+2)(x-$\frac{1}{2}$)ex,
解:∵f′(x)=(x+2)(x-$\frac{1}{2}$)ex,
且f(-2)=$\frac{9}{{2{e^2}}}$,f($\frac{1}{2}$)=$-\frac{{\sqrt{e}}}{2}$,
f(x)的大致图象如图,
令t=f(x),
设方程4e2m2+tm-9$\sqrt{e}$=0的两根为m1,m2,
则m1m2=-$\frac{{9\sqrt{e}}}{{4{e^2}}}$=f(-2)f($\frac{1}{2}$),
若m1=$\frac{9}{{2{e^2}}}$,m2=$-\frac{{\sqrt{e}}}{2}$,有三根;
若0<m1<$\frac{9}{{2{e^2}}}$有三根,此时m2<$-\frac{{\sqrt{e}}}{2}$无根,也有三根,
当m1>$\frac{9}{{2{e^2}}}$有1根,此时$-\frac{{\sqrt{e}}}{2}$<m2<0有两根,也有三根,
故选B.
点评 考查利用导函数分析出的单调性、极值作简图,考查复合函数的零点问题.利用换元法简化方程,考查数形结合.作图、分析根个数,难度较大,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{2}{e}$,+∞) | B. | (-$\frac{2}{e}$,0) | C. | (-∞,-$\frac{2}{e}$) | D. | (-$\frac{2}{e}$,-$\frac{1}{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,M、N、P分别为空间四边形ABCD的边AB,BC,CD上的中点,求证:
如图,M、N、P分别为空间四边形ABCD的边AB,BC,CD上的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 或-2 | B. | 2 | C. | -2 | D. | -1或2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com