
【题目】如图,一幅壁画的最高点![]() 处离地面
处离地面![]() 米,最低点
米,最低点![]() 处离地面
处离地面![]() 米.正对壁画的是一条坡度为
米.正对壁画的是一条坡度为![]() 的甬道(坡度指斜坡与水平面所成角
的甬道(坡度指斜坡与水平面所成角![]() 的正切值),若从离斜坡地面
的正切值),若从离斜坡地面![]() 米的
米的![]() 处观赏它.
处观赏它.
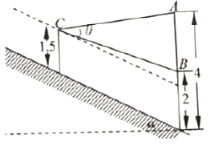
(1)若![]() 对墙的投影(即过
对墙的投影(即过![]() 作
作![]() 的垂线垂足为投影)恰在线段
的垂线垂足为投影)恰在线段![]() (包括端点)上,求点
(包括端点)上,求点![]() 离墙的水平距离的范围;
离墙的水平距离的范围;
(2)在(1)的条件下,当点![]() 离墙的水平距离为多少时,视角
离墙的水平距离为多少时,视角![]() (
(![]() )最大?
)最大?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国境内一座连接中国香港、广东珠海和中国澳门的桥隧工程,因其超大的建筑规模、空前的施工难度以及顶尖的建造技术闻名世界,为内地前往香港的游客提供了便捷的交通途径,某旅行社分年龄统计了大桥落地以后,由香港大桥实现内地前往香港的老中青旅客的比例分别为![]() ,现使用分层抽样的方法从这些旅客中随机抽取
,现使用分层抽样的方法从这些旅客中随机抽取![]() 名,若青年旅客抽到60人,则( )
名,若青年旅客抽到60人,则( )

A.老年旅客抽到150人B.中年旅客抽到20人
C.![]() D.被抽到的老年旅客以及中年旅客人数之和超过200
D.被抽到的老年旅客以及中年旅客人数之和超过200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月17日是我国第6个“扶贫日”,某医院开展扶贫日“送医下乡”医疗义诊活动,现有五名医生被分配到四所不同的乡镇医院中,医生甲被指定分配到医院![]() ,医生乙只能分配到医院
,医生乙只能分配到医院![]() 或医院
或医院![]() ,医生丙不能分配到医生甲、乙所在的医院,其他两名医生分配到哪所医院都可以,若每所医院至少分配一名医生,则不同的分配方案共有( )
,医生丙不能分配到医生甲、乙所在的医院,其他两名医生分配到哪所医院都可以,若每所医院至少分配一名医生,则不同的分配方案共有( )
A.18种B.20种C.22种D.24种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,求曲线
,求曲线![]() 的直角坐标方程以及直线
的直角坐标方程以及直线![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() ,曲线
,曲线![]() 与直线
与直线![]() 交于两点,求
交于两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋子中有红、黄、蓝、绿四个小球,有放回地从中任取一个小球,将“三次抽取后,红色小球,黄色小球都取到”记为事件M,用随机模拟的方法估计事件M发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表红、黄、蓝、绿四个小球,以每三个随机数为一组,表示取小球三次的结果,经随机模拟产生了以下18组随机数:
110 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件M发生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com