
| A�� | p1��p2 | B�� | �Vp1��p2 | C�� | �Vp1��p2 | D�� | p1��p2 |
���� �������������ĵĶ����Լ����������������ж�p1���ⲻ��ʽ�ж�p2���Ӷ�����𰸣�
��� �⣺��������p1����ͼ��ʾ��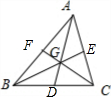
��G�ǡ�ABC�����ģ���$\overrightarrow{AG}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{2}{3}$��$\frac{1}{2}$��$\overrightarrow{AB}$+$\overrightarrow{AC}$��=$\frac{1}{3}$��$\overrightarrow{AB}$+$\overrightarrow{AC}$����
ͬ���ɵã�$\overrightarrow{BG}$=$\frac{1}{3}$��$\overrightarrow{BA}$+$\overrightarrow{BC}$����$\overrightarrow{CG}$=$\frac{1}{3}$��$\overrightarrow{CA}$+$\overrightarrow{CB}$����
��$\overrightarrow{GB}$+$\overrightarrow{GC}$+$\overrightarrow{GA}$=-$\frac{1}{3}$��$\overrightarrow{AB}$+$\overrightarrow{AC}$+$\overrightarrow{BA}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$+$\overrightarrow{CB}$��=$\overrightarrow{0}$��
�������⣻
��������p2���ⲻ��ʽ$\frac{1}{a}$��1�ã�a��1��a��0��
��a��1��$\frac{1}{a}$��1�ij�ֲ���Ҫ�������Ǽ����⣻
��p1��p2�������⣬
��ѡ��D��
���� ���⿼���˳�ֱ�Ҫ�����������������������ʣ��ⲻ��ʽ���⣬��һ�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
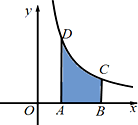 ��ͼ����������ABCD��ֱ��x=1��x=e��x�ἰ����y=$\frac{3}{x}$Χ�ɣ�������������ε������3����ע��eΪ��Ȼ�����ĵ�����
��ͼ����������ABCD��ֱ��x=1��x=e��x�ἰ����y=$\frac{3}{x}$Χ�ɣ�������������ε������3����ע��eΪ��Ȼ�����ĵ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
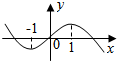 ��֪����f��x��=ax3+bx2+cx+d��ͼ����ͼ��ʾ����f�䣨x����f��x���ĵ���������ʽxf�䣨x����0�Ľ⼯Ϊ��-1��0���ȣ�1��+�ޣ���
��֪����f��x��=ax3+bx2+cx+d��ͼ����ͼ��ʾ����f�䣨x����f��x���ĵ���������ʽxf�䣨x����0�Ľ⼯Ϊ��-1��0���ȣ�1��+�ޣ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Ȳ�����ֲ���Ҫ���� | B�� | ��Ҫ���� | ||
| C�� | ��ֲ���Ҫ���� | D�� | ��Ҫ��������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com