
分析 根据幂函数的性质求出p的值,根据幂函数的单调性得到关于a的不等式解出即可.
解答 解:∵幂函数$y={x}^{{p}^{2}-2p-3}$(p∈N*)在(0,+∞)上是减函数,
∴p2-2p-3<0,解得-1<p<3,
∵p∈N*,
∴p=1或2.
当p=1时,y=x-4为偶函数满足条件,
当p=2时,y=x-3为奇函数不满足条件,
则不等式等价为$({a}^{2}-1)^{\frac{p}{3}}<(3a+3)^{\frac{p}{3}}$,即${{(a}^{2}-1)}^{\frac{1}{3}}$<${(3a+3)}^{\frac{1}{3}}$,
∵y=x$\frac{1}{3}$在(-∞,0)和(0,+∞)上都为增函数,
∴a2-1<3a+3<0或0<a2-1<3a+3,
解得:1<a<4,
故答案为:(1,4).
点评 本题主要考查不等式的求解,根据幂函数的性质求出幂函数的表达式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
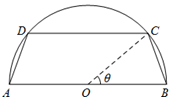 一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,直四棱柱木梁的体积为V(单位:m3),侧面积为S(单位:m2).
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,直四棱柱木梁的体积为V(单位:m3),侧面积为S(单位:m2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1 | C. | x2+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{3}$+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男性 | 女性 | 总计 | |
| 读营养说明 | 40 | 20 | 60 |
| 不读营养说明 | 20 | 20 | 40 |
| 总计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com