
| A. | $\frac{5}{12}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 先求出基本事件总数n=3×4=12,再求出函数f(x)=ax2-2bx在区间(1,+∞)上为增函数满足条件的基本事件个数,由此能求出函数f(x)=ax2-2bx在区间(1,+∞)上为增函数的概率.
解答 解:∵a∈{0,1,2},b∈{-1,1,3,5},
∴基本事件总数n=3×4=12,
函数f(x)=ax2-2bx在区间(1,+∞)上为增函数,
①当a=0时,f(x)=-2bx,符合条件的只有:(0,-1),即a=0,b=-1;
②当a≠0时,需要满足$\frac{b}{a}≤1$,符合条件的有:(1,-1),(1,1),(2,-1),(2,1),共4种,
∴函数f(x)=ax2-2bx在区间(1,+∞)上为增函数的概率是p=$\frac{5}{12}$.
故选:A.
点评 本题考查概率的求不地,是基础题,解题时要认真审题,注意列举法的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$米 | B. | 2$\sqrt{6}$米 | C. | 6米 | D. | 8米 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[kπ-\frac{π}{12},kπ+\frac{5π}{12}](k∈Z)$ | B. | $[kπ+\frac{5π}{12},kπ+\frac{11π}{12}](k∈Z)$ | ||
| C. | $[kπ-\frac{5π}{24},kπ+\frac{7π}{24}](k∈Z)$ | D. | $[kπ+\frac{7π}{24},kπ+\frac{19π}{24}](k∈Z)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
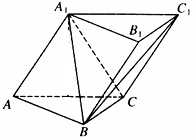 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈R,x2+x+1>0 | B. | ¬p:?x∈R,x2+x+1≠0 | ||
| C. | ¬p:?x∈R,x2+x+1≥0 | D. | ¬p:?x∈R,x2+x+1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36π | B. | 4π | C. | $\frac{27}{4}$π | D. | $\frac{27}{2}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com