
分析 根据一元二次方程根的分布求解即可.
解答 解:方程(m+1)x2+2(2m+1)x+1-3m=0的两根为x1,x2,
∴m+1≠0,
令f(x)=(m+1)x2+2(2m+1)x+1-3m,
∵两根为x1,x2,且x1<1<x2<3,
①当m+1>0时,即m>-1,且f(1)•f(3)<0,
f(1)=m+1+2(2m+1)+1-3m<0,解得:m<-2
f(3)=9(m+1)+6(2m+1)+1-3m>0,解得:m$>-\frac{8}{9}$
此时m无解.
②当m+1<0,即m<-1.且f(1)•f(3)<0,
f(1)=m+1+2(2m+1)+1-3m>0,解得:m<-2
f(3)=9(m+1)+6(2m+1)+1-3m<0,解得:m$<-\frac{8}{9}$
则此可得:-2<m<-1.
故得实数m的取值范围时(-2,-1).
点评 本题主要考查二次方程和二次函数之间的关系,利用二次函数根的分布是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | a≤2$\sqrt{2}$ | B. | a≤2$\sqrt{6}$ | C. | a≤5 | D. | a≤$\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 产量每增加1000件,单位成本下降2.13元 | |
| B. | 产量每减少1000件,单位成本下降2.13元 | |
| C. | 产量每增加1000件,单位成本上升2130元 | |
| D. | 产量每减少1000件,单位成本上升2130元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,点A在平面A1BC中的投影为线段A1B上的点D.
如图所示,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,点A在平面A1BC中的投影为线段A1B上的点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 分析法 | B. | 反证法 | C. | 综合法 | D. | 间接证明法 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
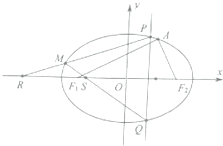 如图,已知椭圆C:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{b}^{2}}=1(0<b<3)$的左、右焦点分别为F1、F2,椭圆上存在一点A,使得AF1=2AF2,且∠F1AF2=90°
如图,已知椭圆C:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{b}^{2}}=1(0<b<3)$的左、右焦点分别为F1、F2,椭圆上存在一点A,使得AF1=2AF2,且∠F1AF2=90°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com