Question

4．已知关于x的方程|x|-2alog₂（|x|+2）+a²=3有唯一实数解，则实数a的值为-1．

Answer 1

分析 构造函数f（x）=|x|-2alog₂（|x|+2）+a²，判断函数是偶函数，根据偶函数的性质先进行求解，然后进行检验即可得到结论．

解答 解：设f（x）=|x|-2alog₂（|x|+2）+a²，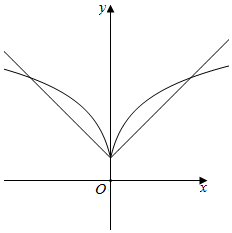
则函数f（x）在定义域（-∞，+∞）上为偶函数，
若关于x的方程|x|-2alog₂（|x|+2）+a²=3有唯一实数解，
则等价为f（0）=3，
即f（0）=-2alog₂2+a²=a²-2a=3，
则a²-2a-3=0，
得a=3或a=-1，
当a=3时，方程等价为|x|-6log₂（|x|+2）+9=3，
即|x|+6=6log₂（|x|+2），
作出函数y=|x|+6和y=6log₂（|x|+2）的图象如图，此时两个函数有3个交点，不满足条件．
当a=-1时，方程等价为|x|+2log₂（|x|+2）+1=3，
即2log₂（|x|+2）=2-|x|，
作出函数y=2-|x|和y=2log₂（|x|+2）的图象如图，此时两个函数有1个交点，满足条件，
综上a=-1，
故答案为：-1．

点评 本题考查了函数的性质的判断与应用及方程的根与函数的关系应用，根据条件构造函数，利用偶函数的对称性建立方程关系求得a值是关键，是中档题也是易错题．