
【题目】某校期中考试后,按照学生的数学考试成绩优秀和不优秀进行统计,得到如下列联表:
优秀 | 不优秀 | 总计 | |
文科 | 60 | 140 | 200 |
理科 | 265 | 335 | 600 |
总计 | 325 | 475 | 800 |
(1)画出列联表的等高条形图,并通过图形判断数学成绩与文理分科是否有关;
(2)利用独立性检验,分析文理分科对学生的数学成绩是否有影响.
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的函数,它的图象关于点(1,0)对称,当x≤1时,f(x)=2xe﹣x(e为自然对数的底数),则f(2+3ln2)的值为( )
A.48ln2
B.40ln2
C.32ln2
D.24ln2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有7名数理化成绩优秀者,其中A1,A2,A3数学成绩优秀,B1,B2物理成绩优秀,C1,C2化学成绩优秀,从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛.
(1)求C1被选中的概率;
(2)求A1,B1不全被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点C在以AB为直径的圆O上,PA垂直于圆O所在的平面,G为△AOC的重心. 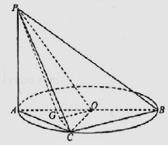
(1)求证:平面OPG⊥平面PAC;
(2)若PA=AB=2AC=2,求二面角A﹣OP﹣G的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数y=f(x)在∈(m,+∞)上的单调性;
(2)若![]() ,则当x∈[m,m+1]时,函数y= f(x)的图象是否总在函数
,则当x∈[m,m+1]时,函数y= f(x)的图象是否总在函数![]() 图象上方?请写出判断过程.
图象上方?请写出判断过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,左右焦点分别为F1 , F2 , 以椭圆短轴为直径的圆与直线
,左右焦点分别为F1 , F2 , 以椭圆短轴为直径的圆与直线 ![]() 相切.
相切.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点F1、斜率为k1的直线l1与椭圆E交于A,B两点,过点F2、斜率为k2的直线l2与椭圆E交于C,D两点,且直线l1 , l2相交于点P,若直线OA,OB,OC,OD的斜率kOA , kOB , kOC , kOD满足kOA+kOB=kOC+kOD , 求证:动点P在定椭圆上,并求出此椭圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三点A(1,﹣1),B(3,0),C(2,1),P为平面ABC上的一点, ![]() =λ
=λ ![]() +μ
+μ ![]() ,且
,且 ![]()
![]() =0,
=0, ![]()
![]() =3.
=3.
(1)求 ![]()
![]() ;
;
(2)求λ+μ 的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.x∈R,2x>x2
B.若a>b,c>d,则 a﹣c>b﹣d
C.x∈R,ex<0
D.ac2<bc2是a<b的充分不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com