
 如图,在四棱锥ABCD-A1B1C1D1中,侧棱AA1⊥平面ABCD,底面ABCD为菱形,∠ABC=120°,AB=AA1=2,AC∩BD=O,E、F分别是线段A1D、BC1的中点,延长D1A1到点G,使得D1A1=AG.
如图,在四棱锥ABCD-A1B1C1D1中,侧棱AA1⊥平面ABCD,底面ABCD为菱形,∠ABC=120°,AB=AA1=2,AC∩BD=O,E、F分别是线段A1D、BC1的中点,延长D1A1到点G,使得D1A1=AG.分析 (1)设AC,BD交点为O,以O为原点建立空间直角坐标系,根据各数量关系求出$\overrightarrow{GB}$和平面DEF的法向量$\overrightarrow{n}$的坐标,只需证明$\overrightarrow{GB}⊥$$\overrightarrow{n}$即可得出GB∥平面DEF;
(2)求出$\overrightarrow{GD}$,计算cos<$\overrightarrow{GD},\overrightarrow{n}$>,于是直线GD与平面DEF所成角的正弦值等于|cos<$\overrightarrow{GD},\overrightarrow{n}$>|.
解答 证明:(1)以O为坐标原点,分别以$\overrightarrow{OB},\overrightarrow{OC}$为x轴,y轴的正方向,建立空间直角坐标O-xyz.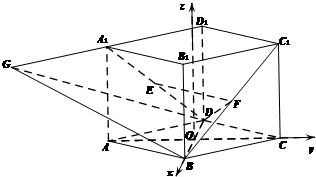
∵在菱形ABCD中,AB=AD=BC=2,∠ABC=120°,
∴BD=2,$AC=2\sqrt{3}$,O为AC和BD的中点.
又AA1⊥平面ABCD,AA1=2.
∴B(1,0,0),D(-1,0,0),${A_1}(0,-\sqrt{3},2)$,${C_1}(0,\sqrt{3},2)$,D1(-1,0,2).
∵E、F分别是线段A1D、BC1的中点,
∴$E(-\frac{1}{2},-\frac{{\sqrt{3}}}{2},1)$,$F(\frac{1}{2},\frac{{\sqrt{3}}}{2},1)$.
∵$\overrightarrow{{D_1}{A_1}}=\overrightarrow{{A_1}G}$,∴$G(1,-2\sqrt{3},2)$.
于是$\overrightarrow{ED}=(-\frac{1}{2},\frac{{\sqrt{3}}}{2},-1)$,$\overrightarrow{EF}=(1,\sqrt{3},0)$,$\overrightarrow{GB}=(0,2\sqrt{3},-2)$.
设平面DEF的一个法向量$\overrightarrow{n}$=(x,y,z).
则$\left\{{\begin{array}{l}{n•\overrightarrow{ED}=0}\\{n•\overrightarrow{EF}=0}\end{array}}\right.$,∴$\left\{\begin{array}{l}{-\frac{1}{2}x+\frac{\sqrt{3}}{2}y-z=0}\\{x+\sqrt{3}y=0}\end{array}\right.$.
令y=-1,得$x=\sqrt{3}$,$z=-\sqrt{3}$.∴$\overrightarrow{n}$=($\sqrt{3}$,-1,-$\sqrt{3}$).
∴$\overrightarrow{GB}•\overrightarrow{n}$=0,∴$\overrightarrow{GB}⊥\overrightarrow{n}$.
又GB?平面DEF,∴GB∥平面DEF.
(2)$\overrightarrow{GD}$=$(-2,2\sqrt{3},-2)$,
∴$\overrightarrow{GD}•\overrightarrow{n}$=-2$\sqrt{3}$,|$\overrightarrow{GD}$|=2$\sqrt{5}$,|$\overrightarrow{n}$|=$\sqrt{7}$.
∴cos<$\overrightarrow{GD},\overrightarrow{n}$>=$\frac{\overrightarrow{GD}•\overrightarrow{n}}{|\overrightarrow{GD}||\overrightarrow{n}|}$=-$\frac{\sqrt{105}}{35}$.
直线GD与平面BEF所成的角的正弦值为|cos<$\overrightarrow{GD},\overrightarrow{n}$>|=$\frac{\sqrt{105}}{35}$.
点评 本题考查了了线面平行的判定,可面角的计算,空间向量的应用,属于中档题.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
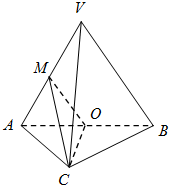 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{15}$ | B. | $\frac{64π}{15}$ | C. | $\frac{15π}{4}$ | D. | $\frac{15π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com