
分析 (1)由同角三角函数恒等式及二倍角公式,可得A=$\frac{π}{3}$.
(2)由正弦定理得到f(x),借助辅助角公式化简后得到单调区间.
解答 解:(Ⅰ)∵cos22A+sin2A=1,
∴cos22A=cos2A,
∴cos2A=±cosA,
∴2cos2A-1±cosA=0,
∵△ABC是锐角三角形,
∴cosA=$\frac{1}{2}$,
∴A=$\frac{π}{3}$.
(Ⅱ)∵BC=1,B=x,
∴AC=$\frac{2\sqrt{3}}{3}$sinx,
AB=cosx+$\frac{\sqrt{3}}{3}$sinx,
∴△ABC的周长f(x)=1+cosx+$\sqrt{3}$sinx=1+2sin(x+$\frac{π}{6}$),
△ABC是锐角三角形,
∴x<$\frac{π}{2}$,C=$\frac{2π}{3}$-x<$\frac{π}{2}$;
∴x∈($\frac{π}{6}$,$\frac{π}{2}$),
∴f(x)的单调增区间是($\frac{π}{6}$,$\frac{π}{3}$],单调减区间是[$\frac{π}{3}$,$\frac{π}{2}$).
点评 本题考查三角函数化简及确定单调区间和正弦定理.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
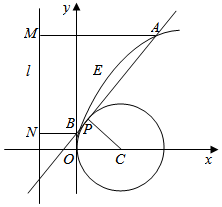 在“2016”的logo设计中,有这样一个图案
在“2016”的logo设计中,有这样一个图案 ,其由线段l、抛物线弧E及圆C三部分组成,对其进行代数化的分析,如图建系,发现:圆C方程为(x-4)2+y2=16,抛物线弧E:y2=2px(y≥0,0≤x≤8),若圆心C恰为抛物线y2=2px的焦点,线段l所在的直线恰为抛物线y2=2px的准线.
,其由线段l、抛物线弧E及圆C三部分组成,对其进行代数化的分析,如图建系,发现:圆C方程为(x-4)2+y2=16,抛物线弧E:y2=2px(y≥0,0≤x≤8),若圆心C恰为抛物线y2=2px的焦点,线段l所在的直线恰为抛物线y2=2px的准线.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有且只有一条 | B. | 有两条 | C. | 有无穷多条 | D. | 必不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
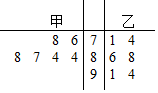 甲,乙两同学在高三上学期的6次联考测试中的物理成绩的茎叶图如图所示,则关于甲,乙两同学的成绩分析正确的是( )
甲,乙两同学在高三上学期的6次联考测试中的物理成绩的茎叶图如图所示,则关于甲,乙两同学的成绩分析正确的是( )| A. | 甲,乙两同学测试成绩的中位数相同 | |
| B. | 甲,乙两同学测试成绩的众数相同 | |
| C. | 甲,乙两同学测试成绩的平均数不相同 | |
| D. | 甲同学测试成绩的标准差比乙同学测试成绩的标准差大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com