
【题目】已知点![]() 为双曲线
为双曲线![]() :
: ![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴上方交双曲线C于点
轴上方交双曲线C于点![]() ,且
,且![]()
(1)求双曲线C的方程;
(2)若直线![]() 与双曲线C恒有两个不同交点P和Q且
与双曲线C恒有两个不同交点P和Q且![]() (其中O为原点),求k的取值范围;
(其中O为原点),求k的取值范围;
(3)过双曲线C上任意一点R作该双曲线两条渐近线的垂线,垂足分别为M,N,求![]() 的值.
的值.
【答案】(1)![]() ;
;
(2)![]() 或
或![]() ;
;
(3)![]() ;
;
【解析】
(1)结合双曲线的定义以及题中的直角三角形,可以得到等量关系![]() ,从而求得
,从而求得![]() ,进而得到
,进而得到![]() ,求得双曲线的方程;
,求得双曲线的方程;
(2)设点![]() ,
,![]() ,将直线方程和双曲线方程联立,消元化简整理,利用判别式大于零,结合题中的条件,求得
,将直线方程和双曲线方程联立,消元化简整理,利用判别式大于零,结合题中的条件,求得![]() 的取值范围;
的取值范围;
(3)先写出双曲线的渐近线方程,设双曲线![]() 上的点
上的点![]() ,设两渐近线的夹角为
,设两渐近线的夹角为![]() ,利用题意求得
,利用题意求得![]() ,又因为点在双曲线上,点的坐标满足双曲线的方程,从而求得
,又因为点在双曲线上,点的坐标满足双曲线的方程,从而求得![]() 的值.
的值.
(1)结合双曲线的定义以及直角三角形的特征
由已知得,![]()
故双曲线![]() 的方程为:
的方程为:![]()
(2)设点![]() ,
,![]() ,
,
联立方程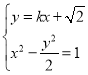 ,得
,得![]() ,
,
因为![]() ,且
,且![]() 解得,
解得,![]() ,且
,且![]() ,
,
![]()
因为![]() ,所以
,所以![]() 故
故![]() ,
,
解不等式![]() 得
得![]() 或
或![]()
综上得,![]() 或
或![]() ;
;
(3)由条件可知:两条渐近线分别为![]() ,
,
设双曲线![]() 上的点
上的点![]() ,
,
设两渐近线的夹角为![]() ,
,
因为 ![]() ,
,
所以![]() ,且
,且![]() ,
,
![]() ,
,
又因为 ![]() ,
,
所以![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】近年来大气污染防治工作得到各级部门的重视,某企业现有设备下每日生产总成本![]() (单位:万元)与日产量
(单位:万元)与日产量![]() (单位:吨)之间的函数关系式为
(单位:吨)之间的函数关系式为![]() ,现为了配合环境卫生综合整治,该企业引进了除尘设备,每吨产品除尘费用为
,现为了配合环境卫生综合整治,该企业引进了除尘设备,每吨产品除尘费用为![]() 万元,除尘后当日产量
万元,除尘后当日产量![]() 时,总成本
时,总成本![]() .
.
(1)求![]() 的值;
的值;
(2)若每吨产品出厂价为59万元,试求除尘后日产量为多少时,每吨产品的利润最大,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
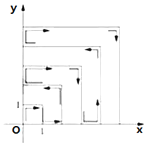
【题目】如图,一个粒子的起始位置为原点,在第一象限内于两正半轴上运动,第一秒运动到(0,1),而后它接着按图示在![]() 轴、
轴、![]() 轴的垂直方向来回运动,且每秒移动一个单位长度,如图所示,经过
轴的垂直方向来回运动,且每秒移动一个单位长度,如图所示,经过![]() 秒时移动的位置设为
秒时移动的位置设为![]() ,那么经过2019秒时,这个粒子所处的位置的坐标是______.
,那么经过2019秒时,这个粒子所处的位置的坐标是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为保护农民种粮收益,促进粮食生产,确保国家粮食安全,调动广大农民粮食生产的积极性,从2004年开始,国家实施了对种粮农民直接补贴.通过对2014~2018年的数据进行调查,发现某地区发放粮食补贴额![]() (亿元)与该地区粮食产量
(亿元)与该地区粮食产量![]() (万亿吨)之间存在着线性相关关系.统计数据如下表:
(万亿吨)之间存在着线性相关关系.统计数据如下表:
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
补贴额 | 9 | 10 | 12 | 11 | 8 |
粮食产量 | 23 | 25 | 30 | 26 | 21 |
(1)请根据如表所给的数据,求出![]() 关于
关于![]() 的线性回归直线方程
的线性回归直线方程![]() ;
;
(2)通过对该地区粮食产量的分析研究,计划2019年在该地区发放粮食补贴额7亿元,请根据(1)中所得的线性回归直线方程,预测2019年该地区的粮食产量.
(参考公式: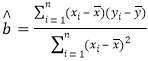 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 到直线
到直线![]() 的距离比它到点
的距离比它到点![]() 的距离大1.
的距离大1.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过定点![]() 作直线
作直线![]() ,与(1)中的轨迹
,与(1)中的轨迹![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 为点
为点![]() 关于原点
关于原点![]() 的对称点,证明:
的对称点,证明:![]() ;
;
(3)在(2)中,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在求出
为直径的圆截得的弦长恒为定值?若存在求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业研制出一种型号为A的精密数控车床,A型车床为企业创造的价值逐年减少(以投产一年的年初到下一年的年初为A型车床所创造价值的第一年).若第 1 年A型车床创造的价值是250万元,且第1年至第6年,每年A型车床创造的价值减少30万元;从第7年开始,每年A型车床创造的价值是上一年价值的 50%.现用![]() (
(![]() )表示A型车床在第n年创造的价值.
)表示A型车床在第n年创造的价值.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)记![]() 为数列
为数列![]() 的前n项的和
的前n项的和![]()
![]() ,企业经过成本核算,若
,企业经过成本核算,若![]() 万元,则继续使用A型车床,否则更换A型车床,试问该企业须在第几年年初更换A型车床?(已知:若正数数列
万元,则继续使用A型车床,否则更换A型车床,试问该企业须在第几年年初更换A型车床?(已知:若正数数列![]() 是单调递减数列,则数列
是单调递减数列,则数列![]() 也是单调递减数列).
也是单调递减数列).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地种植常规稻A和杂交稻B,常规稻A的亩产稳定为500公斤,统计近年来数据得到每年常规稻A的单价比当年杂交稻B的单价高50%.统计杂交稻B的亩产数据,得到亩产的频率分布直方图如下;统计近10年来杂交稻B的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为![]() ,并得到散点图如下,参考数据见下.
,并得到散点图如下,参考数据见下.
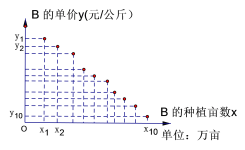
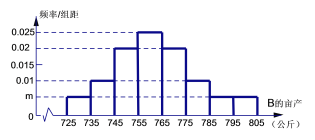
(1)求出频率分布直方图中m的值,若各组的取值按中间值来计算,求杂交稻B的亩产平均值;
(2)判断杂交稻B的单价y(单位:元/公斤)与种植亩数x(单位:万亩)是否线性相关,若相关,试根据以下统计的参考数据求出y关于x的线性回归方程;
(3)调查得到明年此地杂交稻B的种植亩数预计为2万亩,估计明年常规稻A的单价,若在常规稻A和杂交稻B中选择,明年种植哪种水稻收入更高?
统计参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
附:线性回归方程![]() ,
,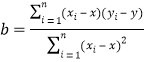 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com