
分析 设P(t,2-t),可得过O、A、P、B的圆的方程与已知圆的方程相减可得AB的方程,进而联立直线方程解方程组可得中点Q的坐标,由点Q到直线的距离公式和不等式的性质可得.
解答 解:∵点P为直线l:x+y=2上的任意一点,∴可设P(t,2-t),
则过O、A、P、B的圆的方程为(x-$\frac{t}{2}$)2+(y-$\frac{2-t}{2}$)2=$\frac{1}{4}$[t2+(2-t)2],
化简可得x2-tx+y2-(2-t)y=0,
与已知圆的方程相减可得AB的方程为tx+(2-t)y=1,
由直线OP的方程为(2-t)x-ty=0,
联立两直线方程可解得x=$\frac{t}{2{t}^{2}-4t+4}$,y=$\frac{2-t}{2{t}^{2}-4t+4}$,
故线段AB的中点Q($\frac{t}{2{t}^{2}-4t+4}$,$\frac{2-t}{2{t}^{2}-4t+4}$),
∴点Q到直线l的距离d=$\frac{|\frac{t}{2{t}^{2}-4t+4}+\frac{2-t}{2{t}^{2}-4t+4}-2|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$|2-$\frac{1}{{t}^{2}-2t+2}$|,
∵t2-2t+2=(t-1)2+1≥1,∴0<$\frac{1}{{t}^{2}-2t+2}$≤1,
∴-1≤-$\frac{1}{{t}^{2}-2t+2}$<0,∴1≤2-$\frac{1}{{t}^{2}-2t+2}$<2,
∴$\frac{\sqrt{2}}{2}$≤$\frac{\sqrt{2}}{2}$|2-$\frac{1}{{t}^{2}-2t+2}$|<$\sqrt{2}$,即d∈[$\frac{\sqrt{2}}{2}$,$\sqrt{2}$)
故答案为:[$\frac{\sqrt{2}}{2}$,$\sqrt{2}$)
点评 本题考查直线与圆的位置关系,涉及圆的相交弦和点到直线的距离公式,以及不等式求函数的值域,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [1,+∞) | C. | [$\frac{4}{3}$,+∞) | D. | [1,$\frac{4}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,G、F分别为EO、EB中点,且AB=$\sqrt{2}$CE.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,G、F分别为EO、EB中点,且AB=$\sqrt{2}$CE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
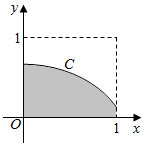 在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )| A. | 3413 | B. | 1193 | C. | 2718 | D. | 6587 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com