
分析 间接法:首先分析题目4个老师分到3个班,每个班至少分到一人,求甲乙两名老师不能分配到同一个班的种数,考虑到应用反面的思想求解,先求出甲乙在一个班的种数,然后用总的种数减去甲乙在一个班的种数,即可得到答案.
直接法:第一步:将四名学生分成3组且甲乙不在同一组求出方法种数,第二步:将3组分配到三个班级有A33=6种方法,由此能求出结果.
解答 解:间接法:考虑用反证法,因为甲、乙两名老师分配到同一个班有3×2=6种排法;
将四名老师分配到三个不同的班,每个班至少分到一名老师有C42•A33=36中排法;
故有甲、乙两名老师不能分配到同一个班有36-6=30种排法.
直接法:第一步:将四名学生分成3组且甲乙不在同一组有C42-1=5种方法,
第二步:将3组分配到三个班级有A33=6种方法,
总的方法种数有5×6=30种.
故答案为:30.
点评 此题主要考查排列组合及简单的计数原理的问题,其中涉及到用反面思想求解的方法,排列组合的问题在高考中多次出现属于重点考点,需要同学们掌握.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
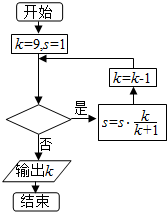
| A. | s>$\frac{1}{2}$ | B. | s>$\frac{3}{5}$ | C. | s>$\frac{7}{10}$ | D. | s>$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
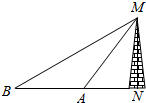 如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )
如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )| A. | 100$\sqrt{2}$m | B. | 100$\sqrt{3}$m | C. | 100m | D. | 200m |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com