
分析 (1)利用参数设出点P,Q的坐标,根据OP,OQ的斜率之积为-$\frac{1}{4}$,可得cos(α-β)=0,确定PQ的中点M的坐标,消去参数,即可求得PQ的中点M的轨迹方程.
(2)设BC方程为my=x+n,利用AB⊥AC,可得BC恒过定点,再求△ABC面积的最大值.
解答 解:(1)设P(4cosα,2sinα),Q(4cosβ,2sinβ).
∵OP,OQ的斜率之积为-$\frac{1}{4}$,
∴$\frac{2sinα}{4cosα}×\frac{2sinβ}{4cosβ}$=-$\frac{1}{4}$
∴cos(α-β)=0,
设M(x,y),则x=2cosα+2cosβ,即$\frac{x}{2}$=cosα+cosβ①,y=sinα+sinβ②
∴①2+②2可得:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1$.
(2)BC斜率不为0,∴可设BC方程为my=x+n,
与椭圆联立得:(m2+4)y2-2mny+n2-8=0,
设B(x1,y1),C(x2,y2),所以y1+y2=$\frac{2mn}{{m}^{2}+4}$,y1y2=$\frac{{n}^{2}-8}{{m}^{2}+4}$,
∴(x1-2$\sqrt{2}$,y1)•(x2-2$\sqrt{2}$,y2)=5n2+16$\sqrt{2}$n+24=0,
∴n=-2$\sqrt{2}$或-$\frac{4\sqrt{2}}{5}$,
当B为左顶点时,△ABC面积为$\frac{1}{2}$×4$\sqrt{2}$×|y1-y2|=$\frac{16|m|}{{m}^{2}+4}$=$\frac{16}{|m|+\frac{4}{|m|}}$≤$\frac{16}{4}$=4,
当且仅当m=±2时,△ABC面积的最大值为4.
点评 本题考查椭圆的方程,考查轨迹方程,考查参数的运用,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题,正确设出点的坐标是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 9 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{21}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 可以做出这样的三角形,且最大内角为$\frac{5π}{6}$ | |
| B. | 可以做出这样的三角形,且最大内角为$\frac{3π}{4}$ | |
| C. | 可以做出这样的三角形,且最大内角为$\frac{2π}{3}$ | |
| D. | 不可能做出这样的三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ② | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
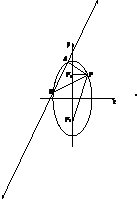 已知F1,F2是椭圆$\frac{y^2}{4}+\frac{x^2}{2}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,直线l:y=$\sqrt{2}$x+m与椭圆交于A,B两点.
已知F1,F2是椭圆$\frac{y^2}{4}+\frac{x^2}{2}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,直线l:y=$\sqrt{2}$x+m与椭圆交于A,B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com