
分析 由已知向量的坐标求得$\overrightarrow{a}+\overrightarrow{b}$的坐标,然后代入数量积求夹角公式得答案.
解答 解:∵$\overrightarrow{a}$=(1,-$\sqrt{3}$),$\overrightarrow{b}$=(3,$\sqrt{3}$),
∴$\overrightarrow{a}+\overrightarrow{b}=(4,0)$,则$|\overrightarrow{a}|=2,|\overrightarrow{a}+\overrightarrow{b}|=4$,$\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$=4,
∴cos$<\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}>$=$\frac{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}{|\overrightarrow{a}||\overrightarrow{a}+\overrightarrow{b}|}=\frac{4}{8}=\frac{1}{2}$,
∴向量$\overrightarrow{a}$与向量$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为60°.
故答案为:60°.
点评 本题考查平面向量的数量积运算,考查了利用数量积求斜率的夹角,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
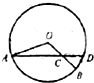 如图,半径为2的⊙O中,∠AOB=120°,C为OB的中点,AC的延长线交⊙O于点D,连接BD,则弦BD的长为( )
如图,半径为2的⊙O中,∠AOB=120°,C为OB的中点,AC的延长线交⊙O于点D,连接BD,则弦BD的长为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{7}}{7}$ | D. | $\frac{3\sqrt{7}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
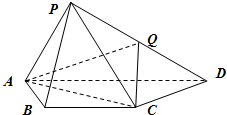 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com