
分析 设∠AFC=θ,$∠BCF=θ-\frac{π}{4}$,在△BCF中,由正弦定理求得丨BC丨,在Rt△ABC中,$|{BC}|=\sqrt{2}|{AC}|=2\sqrt{2}csinθ$,列方程取得θ的正弦及余弦值,分别表示出,|AC|及|AF|,由椭圆的离心率e=$\frac{c}{a}$,代入即可求得椭圆的离心率.
解答 解:如图,设∠AFC=θ,则$∠BCF=θ-\frac{π}{4}$.(F在AB上,F是椭圆的另一个焦点)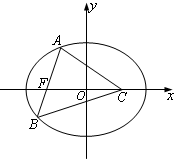
设椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,则|CF|=2c,|AC|=2c•sinθ,|AF|=2c•cosθ.
在△BCF中,由正弦定理和合分比定理,$\frac{{|{BC}|}}{sinθ}=\frac{{|{BF}|}}{{sin(θ-\frac{π}{4})}}=\frac{{|{BC}|+|{BF}|}}{{sinθ+sin(θ-\frac{π}{4})}}=\frac{2a}{{sinθ+sin(θ-\frac{π}{4})}}$.
∴$|{BC}|=2a•\frac{sinθ}{{sinθ+sin(θ-\frac{π}{4})}}$.
在Rt△ABC中,$|{BC}|=\sqrt{2}|{AC}|=2\sqrt{2}csinθ$,
由此得到$2\sqrt{2}csinθ=2a•\frac{sinθ}{{sinθ+sin(θ-\frac{π}{4})}}=2c({sinθ+cosθ})•\frac{sinθ}{{sinθ+sin(θ-\frac{π}{4})}}$,
∴$\sqrt{2}sinθ[sinθ+sin(θ-\frac{π}{4})]=sinθ(sinθ+cosθ)$.
∴$tanθ=\sqrt{2}$,$sinθ=\frac{{\sqrt{6}}}{3}$,$cosθ=\frac{{\sqrt{3}}}{3}$.
∴$\frac{c}{a}=\frac{{|{FC}|}}{{|{AF}|+|{AC}|}}=\frac{2c}{2ccosθ+2csinθ}=\frac{1}{cosθ+sinθ}=\frac{1}{{\frac{{\sqrt{3}}}{3}+\frac{{\sqrt{6}}}{3}}}=\frac{3}{{\sqrt{6}+\sqrt{3}}}=\sqrt{6}-\sqrt{3}$,
故答案为:$\sqrt{6}-\sqrt{3}$.
点评 本题椭圆的离心率的求法,正弦定理及三角恒等变换的综合应用,考查计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-$\sqrt{x}$ | B. | y=log${\;}_{\frac{1}{2}}$x | C. | y=x-3 | D. | y=-x2+2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{7}{25}$ | D. | -$\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 6 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com