
| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | 2$\sqrt{2}$ |
分析 如图,设R,S两点的抛物线的准线上的射影分别为P,Q,过S作PR的垂SG,在三角形RSG中,∠SRG等于直线RS的倾斜角,其正切值即为k值,然后利用抛物线定义结合求解直角三角形求出直线RS的斜率得答案.
解答 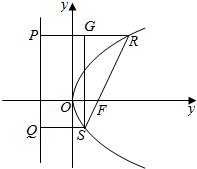 解:如图,设R,S两点的抛物线的准线上的射影分别为P,Q,
解:如图,设R,S两点的抛物线的准线上的射影分别为P,Q,
过S作PR的垂线SG,
在三角形RSG中,∠SRG等于直线RS的倾斜角,其正切值即为k,
设|SF|=n,∵$\overrightarrow{RF}$=2$\overrightarrow{FS}$,
∴|RF|=2|SF|,∴|RF|=2n,
根据抛物线的定义得:|PR|=2n,|SQ|=n,
∴|RG|=n,
在直角三角形RSG中,tan∠SRG=$\frac{|SG|}{|GR|}$=$\frac{\sqrt{9{n}^{2}-{n}^{2}}}{n}$=$2\sqrt{2}$.
故选:D.
点评 本题主要考查了直线与抛物线的位置关系,抛物线的简单性质,特别是焦点弦问题,解题时要注意抛物线定义的灵活运用,是中档题.


科目:高中数学 来源: 题型:填空题
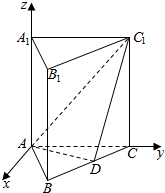 已知正三棱柱ABC-A1B1C1的各棱长均为1,D是BC上一点,AD⊥C1D,以A为坐标原点,平面ABC内AC的垂线,AC,AA1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则点D的坐标为($\frac{\sqrt{3}}{4}$,$\frac{3}{4}$,0),平面ADC1的一个法向量为($\sqrt{3}$,-1,1).
已知正三棱柱ABC-A1B1C1的各棱长均为1,D是BC上一点,AD⊥C1D,以A为坐标原点,平面ABC内AC的垂线,AC,AA1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则点D的坐标为($\frac{\sqrt{3}}{4}$,$\frac{3}{4}$,0),平面ADC1的一个法向量为($\sqrt{3}$,-1,1).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com