
分析 由于直线l:x+y=m过抛物线的焦点,得到直线l的方程,再将l的方程代入抛物线方程y2=2p(x+1)(p>0),消去x,得y2+2py-p2-2p=0,设A(x1,y1),B(x2,y2),由根与系数的关系得y1+y2,y1y2;再由弦长公式|AB|=x1+x2+p,可求得|AB|=4p=3,从而求得p的值.
解答 解:由直线l过抛物线的焦点F($\frac{p}{2}$,0),得直线l的方程为x+y=$\frac{p}{2}$.
代入抛物线方程为y2=2p(x+1)(p>0),消去x,得y2+2py-p2-2p=0.
设直线与抛物线交于A(x1,y1),B(x2,y2),
y1+y2=-2p,y1y2=-p2-2p,
∴|AB|=x1+x2+p=2p-(y1+y2)=4p=3,
解得p=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题考查了抛物线的几何性质以及弦长公式的应用,也考查了一定的计算能力,解题时要灵活运用公式,正确解答.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | 2 | D. | $\frac{\sqrt{5}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3) | B. | (3,+∞) | C. | (-∞,4) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:选择题
已知某空间几何体的正视图,侧视图,俯视图均为如图所示的等腰直角三角形,如果该直角三角形的直角边长为1,那么这个几何体的表面积是( )

A.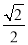 B.
B.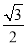
C.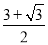 D.
D.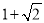
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com