
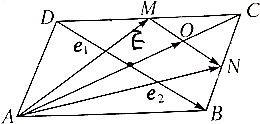
 已知在?ABCD中,M、N分别是DC、BC的中点,若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$,试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$.
已知在?ABCD中,M、N分别是DC、BC的中点,若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$,试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$. 分析 利用向量加法、减法的三角形法则,即可得出结论.
解答 解:由题意,$\overrightarrow{MN}$=$\overrightarrow{AN}$-$\overrightarrow{AM}$=$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$,
∵M、N分别是DC、BC的中点,
∴$\overrightarrow{DB}$=2$\overrightarrow{MN}$,
∴$\overrightarrow{DB}$=2$\overrightarrow{{e}_{2}}$-2$\overrightarrow{{e}_{1}}$,
∵?ABCD中,M、N分别是DC、BC的中点,
∴O是MN的中点,
∴$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AN}$-$\overrightarrow{AM}$)=$\frac{1}{2}$($\overrightarrow{{e}_{2}}$+$\overrightarrow{{e}_{1}}$).
点评 本题主要考查平面向量基本定理及其几何意义,向量加法的三角形法则的应用,体现了数形结合的数学思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 正三棱柱ABC-A1B1C1中,AB=BB1,D是BC的中点.
正三棱柱ABC-A1B1C1中,AB=BB1,D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com