练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．△ABC中，已知cosC=-$\frac{3}{5}$，sinB=$\frac{5}{13}$，则sinA=$\frac{33}{65}$．

    分析 根据两角和差的正弦公式进行求解即可．

    解答 解：在△ABC中，已知cosC=-$\frac{3}{5}$，sinB=$\frac{5}{13}$，
    则$\frac{π}{2}$＜C＜π，则0＜B＜$\frac{π}{2}$，
    则sinC=$\frac{4}{5}$，cosB=$\frac{12}{13}$，
    则sinA=sin[π-（B+C）]=sin（B+C）=sinBcosC+cosBsinC=$\frac{5}{13}$×（-$\frac{3}{5}$）+$\frac{4}{5}$×$\frac{12}{13}$=$\frac{33}{65}$，
    故答案为：$\frac{33}{65}$．

    点评 本题主要考查三角函数值的计算，根据两角和差的正弦公式是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

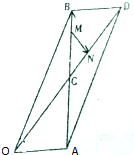    17．如图，平行四边形OADB的对角线OD、AB相交于点C，线段BC上有一点M满足BC=3BM，线段CD上有一点N满足CD=3CN，设|$\overrightarrow{OA}$|=2，|$\overrightarrow{OB}$|=6，∠AOB=60°．
    （1）用向量$\overrightarrow{OA}$，$\overrightarrow{OB}$表示向量$\overrightarrow{MN}$；
    （2）求线段MN的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

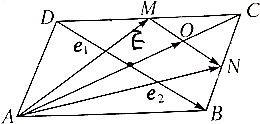    18．已知在?ABCD中，M、N分别是DC、BC的中点，若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$，$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$，试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知点A（1，0），点P是圆C：（x+1）2+y2=8上的任意一点，线段PA的垂直平分线与直线CP交于点E．
    （1）求点E的轨迹方程；
    （2）若直线y=kx+m与点E的轨迹有两个不同的交点P和Q，且原点O总在以PQ为直径的圆的内部，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．定义运算$（\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}）$•$（\begin{array}{l}{e}\\{f}\end{array}）$=$（\begin{array}{l}{ae+bf}\\{ce+df}\end{array}）$，如$（\begin{array}{l}{1}&{2}\\{0}&{3}\end{array}）$•$（\begin{array}{l}{4}\\{5}\end{array}）$=$（\begin{array}{l}{14}\\{15}\end{array}）$．已知α+β=π，α-β=$\frac{π}{2}$，则$（\begin{array}{l}{sinα}&{cosα}\\{cosα}&{sinα}\end{array}）$•$（\begin{array}{l}{cosβ}\\{sinβ}\end{array}）$=（　　）
    A．$（\begin{array}{l}{0}\\{0}\end{array}）$B．$（\begin{array}{l}{0}\\{1}\end{array}）$C．$（\begin{array}{l}{1}\\{0}\end{array}）$D．$（\begin{array}{l}{1}\\{1}\end{array}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知数列{an}的前n项和为Sn，且点（n+1，$\frac{{S}_{n}}{n}$）（n∈N*）在直线y=x上．
    （1）求数列{an}的通项公式；
    （2）求证：$\frac{4}{{{a}_{1}}^{2}}$+$\frac{4}{{{a}_{2}}^{2}}$+…+$\frac{4}{{{a}_{n}}^{2}}$＜2，n∈N*．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知随机变量ξ分别取1、2和3，其中概率p（ξ=1）与p（ξ=3）相等，且方差Dξ=$\frac{1}{3}$，则概率p（ξ=2）的值为$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知数列{an}中，a1=3，a2=5，其前n项和Sn满足Sn+Sn-2=2Sn-1+2n-1 （n≥3）；
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）若bn=nan，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=$\sqrt{3}sinx•cosx-\frac{1}{2}$cos2x（x∈R）．
    （1）求函数f（x）的最小值和最小正周期；
    （2）设△ABC的内角A、B、C的对边分别为a、b、c，且B=30°，c=$\sqrt{3}$，f（C）=1，判断△ABC的形状，并求三角形ABC的面积．

    查看答案和解析>>

    同步练习册答案