Question

12．如图，已知矩形ABCD中，AB=2$\sqrt{2}$，AD=$\sqrt{2}$，M为DC的中点，将△ADM沿AM折起，使得平面ADM⊥平面ABCM．

（1）求证AD⊥BM．；
（2）若E是线段DB的中点，求二面角E-AM-D的余弦值．

Answer 1

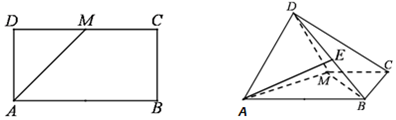
分析 （1）推导出BM⊥AM，BM⊥面ADM，由此能证明BM⊥AD．
（2）以AM中点O为原点，OA为x轴，OD为z轴，建立空间直角坐标系，利用向量法能求出二面角E-AM-D的余弦值．

解答 证明：（1）∵长方形ABCD中，AB=2$\sqrt{2}$，AD=$\sqrt{2}$，M为DC的中点，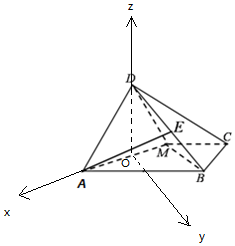
∴AM=BM=2，∴BM⊥AM，
∵面ADM⊥面ABCM，
∴BM⊥面ADM，
∵AD?面ADM，∴BM⊥AD．
解：（2）以AM中点O为原点，OA为x轴，OD为z轴，建立空间直角坐标系，
则A（1，0，0），E（-$\frac{1}{2}$，1，$\frac{1}{2}$），$\overrightarrow{EA}$=（$\frac{3}{2}$，-1，-$\frac{1}{2}$），$\overrightarrow{AM}$=（-2，0，0），
平面AMD的法向量$\overrightarrow{m}$=（0，1，0），
设平面EAM的法向量$\overrightarrow{n}$=（x，y，z），
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EA}=\frac{3}{2}x-y-\frac{1}{2}z=0}\\{\overrightarrow{n}•\overrightarrow{AM}=-2x=0}\end{array}\right.$，取y=1，得$\overrightarrow{n}$=（0，1，-2），
设二面角E-AM-D的平面角为θ，
则cosθ=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$|=$\frac{\sqrt{5}}{5}$．
∴二面角E-AM-D的余弦值为$\frac{\sqrt{5}}{5}$．

点评 本题考查线线垂直的证明，考查二面角的余弦值的求法，是中档题，解题时要认真审题，注意向量法的合理运用．