
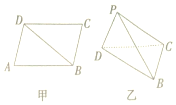
 如图甲,在平行四边形ABCD中,AB=$\sqrt{15}$,AD=$\sqrt{7}$,对角线BD=4,现沿对角线BD把△ABD折起,使点A的位置变成点P,且平面PBD⊥平面BCD如图乙所示,若图乙中三棱锥P-BCD的四个顶点在同一个球的球面上,则该球的表面积为19π.
如图甲,在平行四边形ABCD中,AB=$\sqrt{15}$,AD=$\sqrt{7}$,对角线BD=4,现沿对角线BD把△ABD折起,使点A的位置变成点P,且平面PBD⊥平面BCD如图乙所示,若图乙中三棱锥P-BCD的四个顶点在同一个球的球面上,则该球的表面积为19π. 分析 由余弦定理求出cos∠BCD,得到sin∠BCD,再由正弦定理求出△BCD的外接圆半径,得到△BCD的外接圆圆心到BD的距离d,也就是△PBD的外接圆的圆心到BD的距离,利用勾股定理求得三棱锥P-BCD的外接球的半径,代入球的表面积公式得答案.
解答 解:在△BCD中,由CD=$\sqrt{15}$,BC=$\sqrt{7}$,BD=4,可得cos∠BCD=$\frac{15+7-16}{2\sqrt{105}}=\frac{3}{\sqrt{105}}$,
∴sin∠BCD=$\frac{4\sqrt{6}}{\sqrt{105}}=\frac{4\sqrt{2}}{\sqrt{35}}$,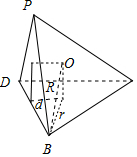
由正弦定理可得△BCD的外接圆半径r=$\frac{\sqrt{70}}{4}$,
则△BCD的外接圆圆心到BD的距离d=$\sqrt{(\frac{\sqrt{70}}{4})^{2}-4}=\frac{\sqrt{6}}{4}$,
同理△PBD的外接圆的圆心到BD的距离也为$\frac{\sqrt{6}}{4}$,
∴三棱锥P-BCD的外接球的半径为R=$\sqrt{(\frac{\sqrt{70}}{4})^{2}+(\frac{\sqrt{6}}{4})^{2}}=\frac{\sqrt{19}}{2}$.
∴该球的表面积为$4π(\frac{\sqrt{19}}{2})^{2}=19π$.
故答案为:19π.
点评 本题考查球的表面积与体积,考查了空间想象能力和思维能力,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com