
分析 (1)由已知条件知,点N是线段FM的中点,NE是线段FM的垂直平分线,点QE的轨迹C是以F为焦点,l为准线的抛物线,写出抛物线标准方程.
(2)求出P,Q的坐标,可得|PQ|,再换元、配方,即可得出结论.
解答 解:(1)依题意知,NE是线段FM的垂直平分线.
∵ME⊥直线l,∴|EM|是点E到直线l的距离.
∵点E在线段FM的垂直平分线,∴|EM|=|EF|.
故动点E的轨迹C是以F为焦点,l为准线的抛物线,其方程为:y2=8x(x>0).
(2)设A(x1,y1),则OA:y=$\frac{{y}_{1}}{{x}_{1}}$x与y=-4-x联立,可得P(-$\frac{4{x}_{1}}{{x}_{1}+{y}_{1}}$,-$\frac{4{y}_{1}}{{x}_{1}+{y}_{1}}$),
同理Q(-$\frac{4{x}_{2}}{{x}_{2}+{y}_{2}}$,-$\frac{4{y}_{2}}{{x}_{2}+{y}_{2}}$)
设AB:x=ty+2与抛物线方程联立,可得y2-8ty-16=0,
∴y1+y2=8t,y1y2=-16
∴|PQ|=$\sqrt{2}$•|x1-x2|=2$\sqrt{2}•|\frac{{y}_{2}-{y}_{1}}{4t+3}|$
=16$\sqrt{2}•\sqrt{\frac{{t}^{2}+1}{(4t+3)^{2}}}$,
令u=4t+3,可得|PQ|=4$\sqrt{2}•\sqrt{25(\frac{1}{u}-\frac{3}{5})^{2}+\frac{16}{25}}$,
∴u=$\frac{5}{3}$,t=-$\frac{1}{3}$时,|PQ|min=$\frac{8\sqrt{2}}{5}$,
x1=2,A(2,4),B(2,-4),P(-$\frac{4}{3}$,-$\frac{8}{3}$),Q(2,-6),
∴|PQ|=$\sqrt{(2+\frac{4}{3})^{2}+(-6+\frac{8}{3})^{2}}$=$\frac{10\sqrt{2}}{3}$$>\frac{8\sqrt{2}}{3}$.
∴线段|PQ|的最小值为$\frac{8\sqrt{2}}{3}$.
点评 本题考查轨迹方程的求法、抛物线的定义、标准方程,以及简单性质的应用,直线过定点问题,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,D,E分别是BC,AC的中点.PB=PC=AB=2,AC=4,BC=2$\sqrt{3}$,PA=$\sqrt{6}$.
如图,三棱锥P-ABC中,D,E分别是BC,AC的中点.PB=PC=AB=2,AC=4,BC=2$\sqrt{3}$,PA=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
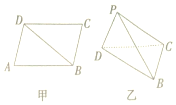 如图甲,在平行四边形ABCD中,AB=$\sqrt{15}$,AD=$\sqrt{7}$,对角线BD=4,现沿对角线BD把△ABD折起,使点A的位置变成点P,且平面PBD⊥平面BCD如图乙所示,若图乙中三棱锥P-BCD的四个顶点在同一个球的球面上,则该球的表面积为19π.
如图甲,在平行四边形ABCD中,AB=$\sqrt{15}$,AD=$\sqrt{7}$,对角线BD=4,现沿对角线BD把△ABD折起,使点A的位置变成点P,且平面PBD⊥平面BCD如图乙所示,若图乙中三棱锥P-BCD的四个顶点在同一个球的球面上,则该球的表面积为19π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,$\frac{1}{3}$) | C. | [$\frac{1}{7}$,$\frac{1}{3}$) | D. | [$\frac{1}{7}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com