
分析 (1)Sn=2an-1,n∈N*;n=1时,a1=S1=2a1-1,解得a1;n≥2时,an=Sn-Sn-1,化为an=2an-1,利用等比数列的通项公式即可得出.
(2)anan+1=2n-1•2n=$\frac{1}{2}×{4}^{n}$.利用等比数列的求和公式即可得出.
(3)由lg2+lg(1+$\frac{1}{{b}_{1}}$)+lg(1+$\frac{1}{{b}_{2}}$)+…+lg(1+$\frac{1}{{b}_{m}}$)=lg(log2am).可得$2×\frac{{b}_{1}+1}{{b}_{1}}$×$\frac{{b}_{2}+1}{{b}_{2}}$×…×$\frac{{b}_{m}+1}{{b}_{m}}$=log2am=m-1.又数列{bn}是连续的正整数数列,bn=bn-1+1.化简进而得出.
解答 解:(1)∵Sn=2an-1,n∈N*;∴n=1时,a1=S1=2a1-1,解得a1=1;
n≥2时,an=Sn-Sn-1=2an-1-(2an-1-1),
化为an=2an-1,∴数列{an}是等比数列,公比为2,首项为1.∴an=2n-1.
(2)anan+1=2n-1•2n=$\frac{1}{2}×{4}^{n}$.
∴Tn=a1a2-a2a3+a3a4-a4a5+…+(-1)n+1anan+1
=$\frac{1}{2}[4-{4}^{2}+$+…+(-1)n+1×4n]
=$\frac{1}{2}×\frac{4[1-(-4)^{n}]}{1-(-4)}$=$\frac{2}{5}$[1-(-4)n].
(3)由lg2+lg(1+$\frac{1}{{b}_{1}}$)+lg(1+$\frac{1}{{b}_{2}}$)+…+lg(1+$\frac{1}{{b}_{m}}$)=lg(log2am).
∴$2×\frac{{b}_{1}+1}{{b}_{1}}$×$\frac{{b}_{2}+1}{{b}_{2}}$×…×$\frac{{b}_{m}+1}{{b}_{m}}$=log2am=m-1.
又数列{bn}是连续的正整数数列,∴bn=bn-1+1.
∴$\frac{2({b}_{m}+1)}{{b}_{1}}$=m-1,又bm=b1+(m-1),
∴mb1-3b1-2m=0,
∴m=$\frac{3{b}_{1}}{{b}_{1}-2}$=3+$\frac{6}{{b}_{1}-2}$,由m∈N*,
∴b1>2,∴b1=3时,m的最大值为9.
∴这些项的和=3+4+…+11=63.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、数列单调性、数列递推关系,考查了推理能力与计算能力,属于难题.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,D,E分别是BC,AC的中点.PB=PC=AB=2,AC=4,BC=2$\sqrt{3}$,PA=$\sqrt{6}$.
如图,三棱锥P-ABC中,D,E分别是BC,AC的中点.PB=PC=AB=2,AC=4,BC=2$\sqrt{3}$,PA=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
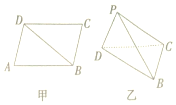 如图甲,在平行四边形ABCD中,AB=$\sqrt{15}$,AD=$\sqrt{7}$,对角线BD=4,现沿对角线BD把△ABD折起,使点A的位置变成点P,且平面PBD⊥平面BCD如图乙所示,若图乙中三棱锥P-BCD的四个顶点在同一个球的球面上,则该球的表面积为19π.
如图甲,在平行四边形ABCD中,AB=$\sqrt{15}$,AD=$\sqrt{7}$,对角线BD=4,现沿对角线BD把△ABD折起,使点A的位置变成点P,且平面PBD⊥平面BCD如图乙所示,若图乙中三棱锥P-BCD的四个顶点在同一个球的球面上,则该球的表面积为19π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com