
| A. | 4 | B. | 6 | C. | 2 | D. | 8 |
分析 由函数f(x)=x2+ax+b(a,b∈R)的图象与x轴相切,可得:△=a2-4b=0,由四边形ABCD是一个以AB,CD为两底,高为5的梯形,S=25=$\frac{1}{2}$(AB+CD)×5,结合韦达定理,构造关于c的方程,解方程可得答案.
解答 解:如图示: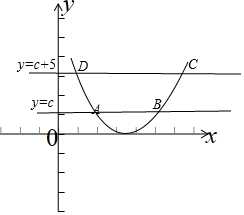 ,
,
∵函数f(x)=x2+ax+b(a,b∈R)的图象与x轴相切,
∴△=a2-4b=0,
设函数f(x)=x2+ax+b的图象与直线y=c交于A,B两点,
即A,B两点的横坐标为方程:x2+ax+b-c=0的两根,
故AB=|x1-x2|=$\sqrt{{{(x}_{1}{+x}_{2})}^{2}-{{4x}_{1}x}_{2}}$=$\sqrt{{a}^{2}-4b+4c}$=2$\sqrt{c}$,
设函数f(x)=x2+ax+b的图象与直线y=c+5交于C,D两点,
同时可得:CD=2 $\sqrt{c+5}$,
此时四边形ABCD是一个以AB,CD为两底,高为5的梯形,
S=25=$\frac{1}{2}$(AB+CD)×5=($\sqrt{c}$+$\sqrt{c+5}$)×5,
即$\sqrt{c}$+$\sqrt{c+5}$=5,
解得:c=4,
故答案为:4.
点评 本题考查的知识点是二次函数的图象和性质,二次方程根与系数的关系,其中由韦达定理及四边形ABCD是一个以AB,CD为两底,高为5的梯形,构造关于c的方程是解答的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
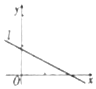 设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),则下列结论正确的是( )
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),则下列结论正确的是( )| A. | x和y成正相关 | |
| B. | 若直线l方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,则$\widehat{b}$>0 | |
| C. | 最小二乘法是使尽量多的样本点落在直线上的方法 | |
| D. | 直线l过点$(\overline x,\overline y)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
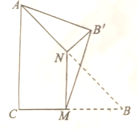 如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )
如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )| A. | $\frac{\sqrt{2}}{5}$ | B. | $\frac{\sqrt{3}}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com