练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    不等式|x＋3|－|x－1|≤a2－3a对任意实数x恒成立，则实数a的取值范围为________．


    (－∞，－1]∪[4，＋∞)

    [解析]　要使|x＋3|－|x－1|≤a2－3a对任意x∈R恒成立，

    则需a2－3a大于等于函数y＝|x＋3|－|x－1|的最大值．

    又ymax＝4，故a2－3a≥4，得a≤－1或a≥4.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    将正奇数按如图所示的规律排列，则第21行从左向右的第5个数为(　　)

    1

    3　5　7

    9　11　13　15　17

    19　21　23　25　27　29　31

    …　…　…

    A．809                                                          B．852

    C．786                                                          D．893

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，矩形ABCD中，AB＝12，AD＝10，将此矩形折叠使点B落在AD边的中点E处，则折痕FG的长为(　　)

    A．13                                                            B. 

    C.                                                            D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中点到圆ρ＝2cosθ的圆心的距离为(　　)

    A．2                                                             B.

    C.                                                    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知曲线C1的参数方程为

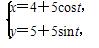    (t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝2sinθ.

    (1)把C1的参数方程化为极坐标方程；

    (2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果关于x的不等式|x－a|＋|x＋4|≥1的解集是全体实数，则实数a的取值范围是(　　)

    A．(－∞，3]∪[5，＋∞)

    B．[－5，－3]

    C．[3,5]

    D．(－∞，－5]∪[－3，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知实数x，y满足：|x＋y|<，|2x－y|<，

    求证：|y|<.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设双曲线－＝1(a>0)的渐近线方程为3x±2y＝0，则a的值为(　　)

    A．4                                                             B．3

    C．2                                                             D．1

    查看答案和解析>>

    同步练习册答案