
分析 (Ⅰ)求出函数的定义域,求导,讨论k的取值,分别解出f′(x)>0,f′(x)<0 即可得出,
(Ⅱ)由(Ⅰ)可求得函数的最小值,f(x0)<$\frac{3}{2}$-k2,将其转化成$\frac{k}{2}$+1-lnk-$\frac{3}{2k}$<0,构造辅助函数,判断其单调性,即可求得k的取值范围.
解答 解:(Ⅰ)f′(x)=x+1-k-$\frac{k}{x}$=$\frac{x2+(1-k)x-k}{x}$=$\frac{(x+1)(x-k)}{x}$,
(ⅰ)k≤0时,f′(x)>0,f(x)在(0,+∞)上单调递增;
(ⅱ)k>0时,x∈(0,k),f′(x)<0;x∈(k,+∞),f′(x)>0,
∴f(x)在(0,k)上单调递减,f(x)在(k,+∞)上单调递增.…(5分)
(Ⅱ)因k>0,由(Ⅰ)知f(x)+k2-$\frac{3}{2}$的最小值为f(k)+k2-$\frac{3}{2}$=$\frac{k2}{2}$+k-klnk-$\frac{3}{2}$,
由题意得$\frac{k2}{2}$+k-klnk-$\frac{3}{2}$<0,即$\frac{k}{2}$+1-lnk-$\frac{3}{2k}$<0.…(8分)
令g(k)=$\frac{k}{2}$+1-lnk-$\frac{3}{2k}$,则g′(k)=$\frac{1}{2}$-$\frac{1}{k}$+$\frac{3}{2k2}$=$\frac{k2-2k+3}{2k2}$>0,
∴g(k)在(0,+∞)上单调递增,又g(1)=0,
∴k∈(0,1)时,g(k)<0,于是$\frac{k2}{2}$+k-klnk-$\frac{3}{2}$<0;
k∈(1,+∞)时,g(k)>0,于是$\frac{k2}{2}$+k-klnk-$\frac{3}{2}$>0.
故k的取值范围为0<k<1.…(12分)
点评 本题主要考查利用导数求函数的单调性研及函数的最值,考查学生分析解决问题的能力,属于中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -e | B. | $\frac{1}{e}$ | C. | e2 | D. | -$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
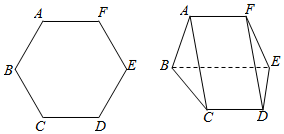 如图,将边长为2的正六边形ABCDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且AC=$\sqrt{6}$,
如图,将边长为2的正六边形ABCDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且AC=$\sqrt{6}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬(p1∨p2) | B. | (¬p2)∨p3 | C. | p3∧(¬p4) | D. | p2∧p4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,+∞) | B. | (-∞,-$\frac{1}{3}$] | C. | [$\frac{1}{3}$,+∞) | D. | (-∞,$\frac{1}{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com