
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 底面
底面![]() ,点
,点![]() 是
是![]() 上的一个动点,
上的一个动点,![]() ,
,![]() .
.

(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)当![]() 平面
平面![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)由已知可得PA![]() 可证
可证![]() 平面
平面![]() ,所以
,所以![]() ,可证
,可证![]() 平面
平面![]() ,从而得到证明;(2)连接
,从而得到证明;(2)连接![]() 交
交![]() 于
于![]() ,当
,当![]() 平面
平面![]() 时,
时,![]() ,以
,以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系.求平面
轴建立空间直角坐标系.求平面![]() 和平面PBD的法向量,利用两个法向量的数量积计算即可得结果.
和平面PBD的法向量,利用两个法向量的数量积计算即可得结果.
(1)因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,
所以![]()
又![]() 为菱形,连接
为菱形,连接![]() 交
交![]() 于
于![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
又因为![]() 平面
平面![]() ,所以
,所以![]() ,又因为
,又因为![]()
![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]()
所以![]() .
.
(2)法一:因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
从而![]() ,
,
![]() 平面
平面![]() ,又因为
,又因为![]() .以
.以![]() 为原点,
为原点,
分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]()
因为![]() ,
,![]() ,
,
由![]() ,
,![]() ,得
,得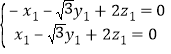 ,
,
令![]() ,则
,则![]() ,
,![]() .
.![]()
设平面![]() 的法向量为
的法向量为![]() ,因为
,因为![]() 平面
平面![]() ,
,
可设![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,由图可知
,由图可知![]() 为锐角,从而
为锐角,从而


法二:因为在平面![]() 中
中![]() ,在平面
,在平面![]() 中,
中,![]() ,
,
从而![]() 为二面角
为二面角![]() 的平面角,
的平面角,
![]()
![]()


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数,
是参数,![]() ),直线
),直线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),曲线
是参数),曲线![]() 与直线
与直线![]() 有一个公共点在
有一个公共点在![]() 轴上,以坐标原点为极点,
轴上,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系
轴的非负半轴为极轴建立极坐标系
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若点![]() ,
,![]() ,
,![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y(万元)的几组对照数据:
x(年) | 2 | 3 | 4 | 5 | 6 |
y(万元) | 1 | 2.5 | 3 | 4 | 4.5 |
(1)若知道y对x呈线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有三家工厂,分别位于矩形ABCD的顶点A,B,及CD的中点P处,已知![]() km,
km,![]() ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
(I)按下列要求写出函数关系式:
①设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
②设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(I)中的一个函数关系式,确定污水处理厂的位置,使三条排水管道总长度最短.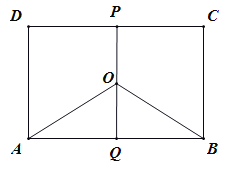
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com