练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．若cosx=-$\frac{2}{3}$，当x∈[0，2π），求角x．

    分析 利用反三角函数求解函数的值即可．

    解答 解：cosx=-$\frac{2}{3}$，当x∈[0，2π），
    可得x=π±arccos$\frac{2}{3}$．

    点评 本题考查反三角函数的求解，三角方程的求法，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．在直角坐标系xOy中，直线C1的参数方程是$\left\{\begin{array}{l}{x=4-\frac{\sqrt{2}}{2}t}\\{y=-1+\frac{\sqrt{2}}{2}t}\end{array}\right.$（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，则曲线C2：ρ=4sinθ
    （Ⅰ）求C1的普通方程和C2的直角坐标方程
    （Ⅱ）判断直线C1与曲线C2的位置关系，若相交，求出弦长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．为了弘扬民族文化，某校举行了“我爱国学，传诵经典”考试，并从图中随机抽取了100名考生的成绩（得分均为整数，满分100分）进行统计制表，其中成绩不低于80分的考生被评为优秀生，请根据频率分布表中所提供的数据，用频率估计概率，回答下列问题．
    分组频数频率
    [50，60）50.05
    [60，70）a0.20
    [70，80）35b
    [80，90）250.25
    [90，100）150.15
    合计1001.00
    （1）求a，b的值并估计这100名考生成绩的平均分；
    （2）按频率分布表中的成绩分组，采用分层抽样抽取20人参加学校的“我爱国学”宣传活动，求其中优秀生的人数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．命题：?x∈R，x2+x-1≥0的否定是（　　）
    A．?x0∈R，x02+x0-1≥0B．?x0∈R，x02+x0-1＜0
    C．?x∈R，x2+x-1≤0D．?x∈R，x2+x-1＜0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在长方体ABCD-A1B1C1D1中，AB=AD=3cm，AA1=2cm，点E为AA1中点，则三棱锥E-D1DB1的体积为3cm3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．若函数f（x）=tan（ωx-$\frac{π}{3}$）（ω＞0）的最小正周期为$\frac{π}{2}$，则函数f（x）的一个单调递增区间是（　　）
    A．（-$\frac{π}{6}$，$\frac{π}{12}$）B．（$\frac{π}{4}$，$\frac{7π}{12}$）C．（$\frac{π}{3}$，$\frac{5π}{6}$）D．（-$\frac{7π}{12}$，-$\frac{π}{12}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．如图1是四棱锥的直观图，其正（主）视图和侧（左）视图均为直角三角形，俯视图外框为矩形，相关数据如图2所示．

    （1）设AB中点为O，在直线PC上找一点E，使得OE∥平面PAD，并说明理由；
    （2）若直线PB与底面ABCD所成角的正切值为$\frac{{2\sqrt{5}}}{5}$，求四棱锥P-ABCD的外接球的表面积．

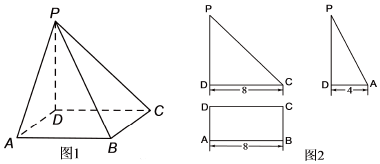
    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知a=${∫}_{0}^{1}$$\sqrt{x}$dx，b=${∫}_{0}^{1}$xdx，c=${∫}_{0}^{1}$x2dx，则a，b，c的大小关系是（　　）
    A．c＜b＜aB．a＜c＜bC．b＜a＜cD．c＜a＜b

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．如图，△AOB为等腰直角三角形，OA=l，OC为斜边AB的髙，点P在射线OC 上，则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为（　　）
    A．-1B．-$\frac{1}{4}$C．-$\frac{1}{8}$D．0

    查看答案和解析>>

    同步练习册答案