
分析 (Ⅰ)由a2是S2与1的等差中项列式求出首项,则{an}是以1为首项,2为公比的等比数列.由等比数列的通项公式得答案;
(Ⅱ)由(Ⅰ)可得:$\frac{1}{{a}_{n}}=(\frac{1}{2})^{n-1}$,说明数列{$\frac{1}{{a}_{n}}$}是以1为首项,以$\frac{1}{2}$为公比的等比数列,则数列{$\frac{1}{{a}_{n}}$}的前n项和为Tn可求,结合Tn<λ恒成立求得实数λ的最小值.
解答 解:(Ⅰ)∵an+1=2an(n∈N*),
∴S2=a1+a2=a1+2a1=3a1,
则4a1=3a1+1,a1=1.
∴{an}是以1为首项,2为公比的等比数列.
∴${a}_{n}=1×{2}^{n-1}={2}^{n-1}$;
(Ⅱ)由(Ⅰ)可得:$\frac{1}{{a}_{n}}=(\frac{1}{2})^{n-1}$,
∴$\frac{1}{{a}_{1}}=1$,$\frac{1}{{a}_{n+1}}=\frac{1}{2}•\frac{1}{{a}_{n}}$,
∴数列{$\frac{1}{{a}_{n}}$}是以1为首项,以$\frac{1}{2}$为公比的等比数列.
∴数列{$\frac{1}{{a}_{n}}$}的前n项和为Tn=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}=2(1-\frac{1}{{2}^{n}})$.
∵$\frac{1}{{2}^{n}}>0$,∴${T}_{n}=2(1-\frac{1}{{2}^{n}})<2$.
∴对任意n∈N*,Tn<λ恒成立,则λ≥2.
∴实数λ的最小值为2.
点评 本题考查等比数列的通项公式,考查了等差数列的性质,考查了等比数列的前n项和,是中档题.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:解答题
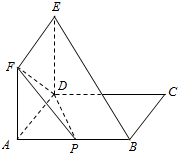 如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.
如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①是类比推理,②是归纳推理 | B. | ①是类比推理,②是演绎推理 | ||
| C. | ①是归纳推理,②是演绎推理 | D. | ①是演绎推理,②是类比推理 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
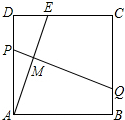 在祖国60年国庆庆典晚会上,需制作表演道具,如图.将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E,使DE=5,折痕为PQ,则线段PM和MQ的比是( )
在祖国60年国庆庆典晚会上,需制作表演道具,如图.将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E,使DE=5,折痕为PQ,则线段PM和MQ的比是( )| A. | 5:12 | B. | 5:13 | C. | 5:19 | D. | 5:21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com