
分析 寻找使不等式:(a+2)2+(b+2)2≥$\frac{25}{2}$成立的充分条件,直到使不等式成立的充分条件已经显然具备为止.
解答 证明:要证:(a+2)2+(b+2)2≥$\frac{25}{2}$,
只要证:a2+b2+4(a+b)+8≥$\frac{25}{2}$,
∵a+b=1,
∴只要证a2+b2≥$\frac{1}{2}$,
∴即证a2+(1-a)2≥$\frac{1}{2}$
只要证(a-$\frac{1}{2}$)2≥0,
显然成立,故原不等式成立.
点评 本题主要考查基本不等式的应用,用分析法证明不等式,利用用分析法证明不等式的关键是寻找使不等式成立的充分条件,直到使不等式成立的充分条件已经显然具备为止,属于中档题.


 新课标同步训练系列答案
新课标同步训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
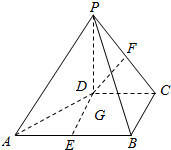 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=CB=1,BA=2,AB∥DC,∠BCD=90°,点E、F、G分别是线段AB、PC、DE的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=CB=1,BA=2,AB∥DC,∠BCD=90°,点E、F、G分别是线段AB、PC、DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com