Question

14．在直角坐标系xoy中，曲线C的参数方程为$\left\{\begin{array}{l}x=sinα-cosα\\ y=sin2α\end{array}\right.（α$为参数），若以原点O为极点、x轴的正半轴为极轴建立极坐标系，曲线E的极坐标方程为$ρsin（θ-\frac{π}{4}）=\sqrt{2}m$，若曲线C与曲线E有且只有一个公共点，则实数m的值为$[-\frac{{\sqrt{2}+1}}{2}，\frac{{\sqrt{2}-1}}{2}）∪\left\{{\frac{5}{8}}\right\}$．

Answer 1

分析 化参数方程、极坐标方程为普通方程，利用曲线C与曲线E有且只有一个公共点，推出结果即可．

解答 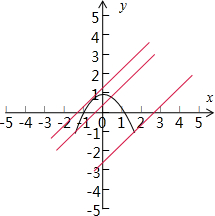解：由$\left\{\begin{array}{l}x=sinα-cosα\\ y=sin2α\end{array}\right.⇒y=1-{x^2}（-\sqrt{2}≤x≤\sqrt{2}）$，
曲线E的直角坐标方程为直线l：x-y+2m=0，
当直线与抛物线段相切时，由$\left\{\begin{array}{l}y=1-{x^2}\\ y=x+2m\end{array}\right.⇒{x^2}+x+2m-1=0⇒△=1-4（2m-1）=0⇒m=\frac{5}{8}$，
可得公共点为$（-\frac{1}{2}，\frac{3}{4}）$满足题目的条件；而抛物线段的两个端点为$A（-\sqrt{2}，-1）、B（\sqrt{2}，-1）$，
当直线过点A时可求得$m=\frac{{\sqrt{2}-1}}{2}$，当直线过点B时可求得$m=-\frac{{\sqrt{2}+1}}{2}$，由图可知，
当$-\frac{{\sqrt{2}+1}}{2}≤m＜\frac{{\sqrt{2}-1}}{2}$时，直线l与抛物线段有唯一的公共点．
故答案为：$[-\frac{\sqrt{2}+1}{2}，\frac{\sqrt{2}-1}{2}）∪\left\{\frac{5}{8}\right\}$．

点评 本题考查直线与抛物线的参数方程、极坐标方程的应用，直线与抛物线的位置关系，考查计算能力．