
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{7\sqrt{2}}}{10}$ |
分析 利用同角三角的基本关系求得cosα,再利用两角和的正弦公式求得f(α+$\frac{π}{12}}$)的值.
解答 解:∵f(x)=sin(x+$\frac{π}{6}$),sinα=$\frac{3}{5}$(0<α<$\frac{π}{2}}$),
∴cosα=$\sqrt{{1-sin}^{2}α}$=$\frac{4}{5}$,
∴f(α+$\frac{π}{12}}$)=sin(α+$\frac{π}{12}$+$\frac{π}{6}$)=sin(α+$\frac{π}{4}$)=sinα•$\frac{\sqrt{2}}{2}$+cosα$\frac{\sqrt{2}}{2}$=$\frac{7\sqrt{2}}{10}$,
故选:D.
点评 本题主要考查同角三角的基本关系,两角和的正弦公式的应用,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin(α+β)=sinα+sinβ | B. | cos(α+β)=cosαcosβ+sinβsinβ | ||
| C. | tan(α+β)=$\frac{tanα-tanβ}{1-tanαtanβ}$ | D. | sin(α+β)sin(α-β)=sin2α-sin2β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
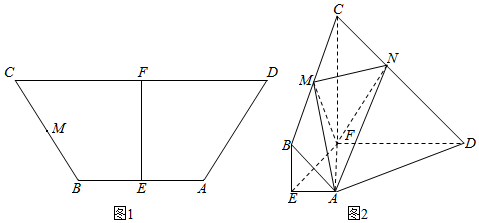
 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知:∠ABC=45°,AB=2,$BC=2\sqrt{2}$,SB=SC,直线SA与平面ABCD所成角为45°,O为BC的中点.
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知:∠ABC=45°,AB=2,$BC=2\sqrt{2}$,SB=SC,直线SA与平面ABCD所成角为45°,O为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22016-1 | B. | 3•21008-3 | C. | 3•21008-1 | D. | 3•21007-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
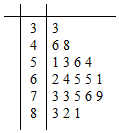 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
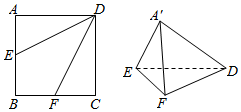 如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′.
如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com