
【题目】已知集合 ![]() ,设f:x→2x﹣3是集合C={﹣1,1,n}到集合B={﹣5,﹣1,3}的映射.
,设f:x→2x﹣3是集合C={﹣1,1,n}到集合B={﹣5,﹣1,3}的映射.
(1)若m=5,求A∩C;
(2)若﹣2∈A,求m的值.
【答案】
(1)解:∵m=5,
∴ ![]() ,m2﹣3m=10,
,m2﹣3m=10,
则A={0,1,3,10},
设f:x→2x﹣3是集合C={﹣1,1,n}到集合B={﹣5,﹣1,3}的映射,
∵2n﹣3=3,得n=3,
则C={﹣1,1,3},
A∩C={1,3}
(2)解:根据题意,m2+2≥2,则log3(m2+2)>0,
若﹣2∈A,必有m2﹣3m=﹣2,
解可得m=1或m=2,
当m=1, ![]() ,不合集合元素的互异性,舍去;
,不合集合元素的互异性,舍去;
当m=2, ![]() ,符合集合性质.
,符合集合性质.
综上,m的值为2
【解析】(1)、根据题意,由m=5计算可得 ![]() ,m2﹣3m=10,即可得集合A,同时分析可得n的值,可得集合C,由集合交集的定义,计算即可得答案;(2)、根据题意,分析集合A的元素,可得m2﹣3m=﹣2,解可得m的值,将m的值代入集合A,分析其元素是否满足集合中元素的特点,即可得答案.
,m2﹣3m=10,即可得集合A,同时分析可得n的值,可得集合C,由集合交集的定义,计算即可得答案;(2)、根据题意,分析集合A的元素,可得m2﹣3m=﹣2,解可得m的值,将m的值代入集合A,分析其元素是否满足集合中元素的特点,即可得答案.
【考点精析】掌握元素与集合关系的判断是解答本题的根本,需要知道对象![]() 与集合
与集合![]() 的关系是
的关系是![]() ,或者
,或者![]() ,两者必居其一.
,两者必居其一.


科目:高中数学 来源: 题型:
【题目】已知命题p:函数 ![]() 在区间(m,m+1)上单调递减,命题q:实数m满足方程
在区间(m,m+1)上单调递减,命题q:实数m满足方程 ![]() 表示的焦点在y轴上的椭圆.
表示的焦点在y轴上的椭圆.
(1)当p为真命题时,求m的取值范围;
(2)若命题“p且q”为假命题,“p或q”为真命题,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆 ![]() (m>n>0)的离心率e的值为
(m>n>0)的离心率e的值为 ![]() ,右准线方程为x=4.如图所示,椭圆C左右顶点分别为A,B,过右焦点F的直线交椭圆C于M,N,直线AM,MB交于点P.
,右准线方程为x=4.如图所示,椭圆C左右顶点分别为A,B,过右焦点F的直线交椭圆C于M,N,直线AM,MB交于点P. 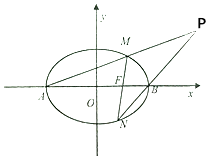
(1)求椭圆的标准方程;
(2)若点P(4, ![]() ),直线AN,BM的斜率分别为k1 , k2 , 求
),直线AN,BM的斜率分别为k1 , k2 , 求 ![]() .
.
(3)求证点P在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() ,若f(x)≤g(x)在区间[0,1]上恒成立,则( )
,若f(x)≤g(x)在区间[0,1]上恒成立,则( )
A.实数t有最小值1
B.实数t有最大值1
C.实数t有最小值 ![]()
D.实数t有最大值 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:①、若m>0,则方程x2﹣x+m=0有实根. ②、若x>1,y>1,则x+y>2的逆命题. ③、对任意的x∈{x|﹣2<x<4},|x﹣2|<3的否定形式. ④、△>0是一元二次方程ax2+bx+c=0有一正根和一负根的充要条件.是真命题的有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】建造一间地面面积为12m2的背面靠墙的猪圈,底面为长方形的猪圈正面的造价为120元/m2 , 侧面的造价为80元/m2 , 屋顶造价为1120元.如果墙高3m,且不计猪圈背面的费用,问怎样设计能使猪圈的总造价最低,最低总造价是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017安徽阜阳二模】一企业从某生产线上随机抽取![]() 件产品,测量这些产品的某项技术指标值
件产品,测量这些产品的某项技术指标值![]() ,得到的频率分布直方图如图.
,得到的频率分布直方图如图.
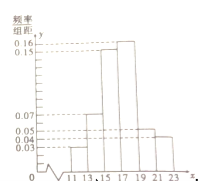
(1)估计该技术指标值![]() 平均数
平均数![]() ;
;
(2)在直方图的技术指标值分组中,以![]() 落入各区间的频率作为
落入各区间的频率作为![]() 取该区间值的频率,若
取该区间值的频率,若![]() ,则产品不合格,现该企业每天从该生产线上随机抽取
,则产品不合格,现该企业每天从该生产线上随机抽取![]() 件产品检测,记不合格产品的个数为
件产品检测,记不合格产品的个数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且OB=(1+ ![]() )百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°.设OA=x(3≤x≤6)百米,OC=y百米.
)百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°.设OA=x(3≤x≤6)百米,OC=y百米.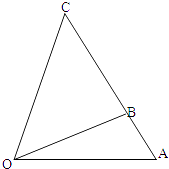
(1)试将y表示成x的函数,并求出函数y的解析式;
(2)当x取何值时?整个中转站的占地面积S△OAC最小,并求出其面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com