Question

【题目】己知椭圆 （m＞n＞0）的离心率e的值为 ，右准线方程为x=4．如图所示，椭圆C左右顶点分别为A，B，过右焦点F的直线交椭圆C于M，N，直线AM，MB交于点P．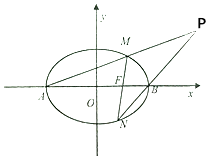

（1）求椭圆的标准方程；
（2）若点P（4， ），直线AN，BM的斜率分别为k1 ， k2 ， 求 ．
（3）求证点P在一条定直线上．

Answer 1

【答案】
（1）解：∵椭圆 （a＞b＞0）的离心率e的值为 ，即 ，右准线方程为x=4，即

解得：a=2，c=1，

∵a2=b2+c2

∴b= ．

故得椭圆的标准方程为：

（2）解：点P（4，3 ），A（﹣2，0），故得直线AP方程为y= ，与椭圆方程 联立，求解M的坐标为（0， ），

那么可得MN直线方程为y=1﹣3x，与椭圆方程 联立，求解N的坐标为（ ， ），

那么AN的斜率为k1= ，BM的斜率k2= ，则 =

（3）解：设斜率存在的MN的直线方程为y=k（x﹣1），利用设而不求的思想，M（x1，y1），N（x2，y2），

与椭圆方程 联立，可得：（4k2+3）x2﹣8k2x+4k2﹣12=0，

那么： …①， …②

由A，M的坐标可得直线AM的方程为 ，

由B，N的坐标可得直线BN的方程为 ，4

直线AM与直线BN联立，可得： ，

∴ …③，

将①②代入③

解得：x=4．

故点P在直线x=4上．

当k不存在时，经验证，点P在直线x=4上满足题意

【解析】（1）利用椭圆C的离心率为 ，右准线的方程为x=4，建立方程，求出几何量，可得椭圆C的方程；（2）利用A，P点，求出直线AP，与椭圆方程求解M的坐标，直线MF与椭圆联立求出N的坐标，可得AN，BM的斜率分别为k1 ， k2 ， 可求 的值．（3）设出MN的直线方程y=k（x﹣1），利用设而不求的思想，M（x1 ， y1），N（x2 ， y2），表示出AN直线，BM直线的方程．AN直线与BM直线联立方程求解p的坐标，可得P在一条定直线上．