
【题目】设![]() ,函数
,函数![]() .
.
(Ⅰ)若![]() ,求曲线
,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() 无零点,求实数
无零点,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() 有两个相异零点
有两个相异零点![]() ,求证:
,求证: ![]() .
.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() ;(Ⅲ)证明见解析.
;(Ⅲ)证明见解析.
【解析】试题分析:
(Ⅰ)首先求得函数的导数,然后利用导函数研究函数的切线可得曲线![]() 在
在![]() 处的切线方程是
处的切线方程是![]() ;
;
(Ⅱ)结合函数的解析式分类讨论可得实数![]() 的取值范围是
的取值范围是![]() ;
;
(Ⅲ)由题意结合题中的结论构造函数![]() 即可证得题中的不等式.
即可证得题中的不等式.
试题解析:
(Ⅰ)函数的定义域为![]() ,
,
当![]() 时,
时, ![]() ,则切线方程为
,则切线方程为![]() ,即
,即![]() .
.
(Ⅱ)①若![]() 时,则
时,则![]() 是区间
是区间![]() 上的增函数,
上的增函数,
∵![]() ,
,
∴![]() ,函数
,函数![]() 在区间
在区间![]() 有唯一零点;
有唯一零点;
②若![]() 有唯一零点
有唯一零点![]() ;
;
③若![]() ,令
,令![]() ,得
,得![]() ,
,
在区间![]() 上,
上, ![]() ,函数
,函数![]() 是增函数;
是增函数;
在区间![]() 上,
上, ![]() ,函数
,函数![]() 是减函数;
是减函数;
故在区间![]() 上,
上, ![]() 的最大值为
的最大值为![]() ,
,
由于![]() 无零点,须使
无零点,须使![]() ,解得
,解得![]() ,
,
故所求实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)设![]() 的两个相异零点为
的两个相异零点为![]() ,设
,设![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,要证
,要证![]() ,只需证
,只需证![]() ,
,
只需![]() ,等价于
,等价于![]() ,
,
设![]() 上式转化为
上式转化为![]() ),
),
设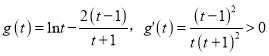 ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)在给定的直角坐标系内画出f(x)的图象; 
(2)写出f(x)的单调递增区间和最值及取得最值时x的值(不需要证明);
(3)若方程f(x)﹣a=0,有三个实数根,求a的取 值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累积净化量![]() ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据![]() 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量![]() 有如下等级划分:
有如下等级划分:
累积净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器(共5000台)的质量,随机抽取![]() 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这![]() 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在![]() 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
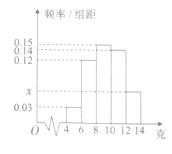
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累积净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() ,已知
,已知![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 位于第一象限.
位于第一象限.
(Ⅰ)求点![]() 和点
和点![]() 的极坐标;
的极坐标;
(Ⅱ)设圆![]() 的圆心为
的圆心为![]() ,点
,点![]() 是直线
是直线![]() 上的动点,且满足
上的动点,且满足![]() ,若直线
,若直线![]() 的参数方程为
的参数方程为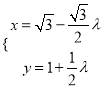 (
(![]() 为参数),则
为参数),则![]() 的值为多少?
的值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下结论正确的是( )
A.若a<b且c<d,则ac<bd
B.若ac2>bc2 , 则a>b
C.若a>b,c<d,则a﹣c<b﹣d
D.若0<a<b,集合A={x|x= ![]() },B={x|x=
},B={x|x= ![]() },则A?B
},则A?B
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线C:y2=2px和⊙M:(x﹣4)2+y2=1,过抛物线C上一点H(x0 , y0)(y0≥1)作两条直线与⊙M相切于A、两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为 ![]() .
.
(Ⅰ)求抛物线C的方程;
(Ⅱ)当∠AHB的角平分线垂直x轴时,求直线EF的斜率;
(Ⅲ)若直线AB在y轴上的截距为t,求t的最小值.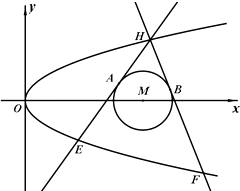
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆 ![]() (m>n>0)的离心率e的值为
(m>n>0)的离心率e的值为 ![]() ,右准线方程为x=4.如图所示,椭圆C左右顶点分别为A,B,过右焦点F的直线交椭圆C于M,N,直线AM,MB交于点P.
,右准线方程为x=4.如图所示,椭圆C左右顶点分别为A,B,过右焦点F的直线交椭圆C于M,N,直线AM,MB交于点P. 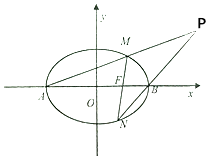
(1)求椭圆的标准方程;
(2)若点P(4, ![]() ),直线AN,BM的斜率分别为k1 , k2 , 求
),直线AN,BM的斜率分别为k1 , k2 , 求 ![]() .
.
(3)求证点P在一条定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com