
分析 (1)利用等差数列的通项与求和公式,建立方程,求出首项与公差,即可求数列{an}的通项;利用等比数列的通项公式,可求数列{bn}的通项公式;
(2)利用错位相减法,可求数列{an•bn}的前n项和Tn.
解答 解:(1)设公差为d,则由a2=5,S5=40,得:$\left\{{\begin{array}{l}{{a_1}+d=5}\\{{a_1}+2d=8}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{{a_1}=2}\\{d=3}\end{array}}\right.$,则an=3n-1…(4分)
(2)∵${q^3}=\frac{b_4}{b_1}=\frac{81}{3}=27$∴q=3${b_n}={b_1}{q^{n-1}}=3•{3^{n-1}}={3^n}$…(8分)
(3)${T_n}={c_1}+{c_2}+{c_3}+…+{c_n}=2×3+5×{3^2}+8×{3^3}+…+(3n-1){3^n}$①
∴$3{T_n}=2×{3^2}+5×{3^3}+8×{3^4}+…+(3n-1){3^{n+1}}$②
①-②:$-2{T_n}=2×3+3({3^2}+{3^3}+…+{3^n})-(3n-1){3^{n+1}}$
∴${T_n}=\frac{{(6n-5){3^{n+1}}+15}}{4}$…(14分)
点评 本题考查等差数列与等比数列的通项,考查数列的求和,考查错位相减法的运用,确定数列的通项是关键.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
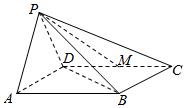 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a2≥b,则a≥$\sqrt{b}$或a≤-$\sqrt{b}$ | B. | 若a2≥b,则a>$\sqrt{b}$或a<-$\sqrt{b}$ | ||
| C. | 若a≥$\sqrt{b}$或a≤-$\sqrt{b}$,则a2≥b | D. | 若a>$\sqrt{b}$或a<-$\sqrt{b}$,则a2≥b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$$\sqrt{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com