练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （2014•潍坊三模）为了解某班学生喜爱打篮球是否与性别有关，对该班50名学生进行了问卷调查，得到如下的2×2列联表．

     

    喜爱打篮球

    不喜爱打篮球

    合计

    男生

    20

    5

    25

    女生

    10

    15

    25

    合计

    30

    20

    50

    则至少有（ ）的把握认为喜爱打篮球与性别有关．

    A.95% B.99% C.99.5% D.99.9%

     

    C

    【解析】

    试题分析：根据所给的列联表得到求观测值所用的数据，把数据代入观测值公式中，做出观测值，同所给的临界值表进行比较，得到所求的值所处的位置，得到百分数．

    【解析】
    根据所给的列联表，

    得到k2==8.333＞7.879，

    ∴至少有99.5%的把握说明喜爱打篮球与性别有关．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年人教A版选修四4-1第一讲1.2练习卷（解析版） 题型：填空题

    （2014•湖北）如图，D是△ABC中BC边上一点，点E、F分别是△ABD，△ACD的重心，EF与AD交于点M，则= ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修一1-2第四章4.2练习卷（解析版） 题型：选择题

    如图是《集合》的知识结构图，如果要加入“子集”，则应该放在（ ）

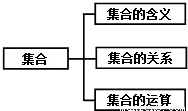
    A.“集合”的下位 B.“集合的含义”的下位

    C.“集合的关系”的下位 D.“基本的运算”的下位

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修一1-2第一章1.2练习卷（解析版） 题型：选择题

    （2012•枣庄一模）通过随机询问100名性别不同的大学生是否爱好踢毪子运动，得到如下的列联表：

     

    男

    女

    总计

    爱好

    10

    40

    50

    不爱好

    20

    30

    50

    总计

    30

    70

    100

    附表：

    P（K2≥k）

    0.10

    0.05

    0.025

    k

    2.706

    3.841

    5.024

    随机变量，经计算，统计量K2的观测值k≈4.762，参照附表，得到的正确结论是（ ）

    A.在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别有关”

    B.在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别无关”

    C.有97.5%以上的把握认为“爱好该项运动与性别有关”

    D.有97.5%以上的把握认为“爱好该项运动与性别无关”

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修一1-2第一章1.2练习卷（解析版） 题型：选择题

    （2014•黄山二模）某部门为了了解青年人喜欢户外运动是否与性别有关，运用2×2列联表进行独立性检验，经计算K2=7.069，则所得到的统计学结论为：有（ ）把握认为“喜欢户外运动与性别有关”．

    附：（独立性检验临界值表）

    P（K2≥k0）

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    3.841

    5.024

    6.636

    7.879

    10.828

    A.0.1% B.1% C.99% D.99.9%

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修一1-2第一章1.1练习卷（解析版） 题型：选择题

    （2014•上饶二模）某学生在高三学年最近九次考试中的数学成绩加下表：

    第x考试

    1

    2

    3

    4

    5

    6

    7

    8

    9

    数学成绩y（分）

    121

    119

    130

    106

    131

    123

    110

    124

    116

    设回归直线方程y=bx+a，则点（a，b）在直线x+5y﹣10=0的（ ）

    A.左上方 B.左下方 C.右上方 D.右下方

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修一1-2第一章1.1练习卷（解析版） 题型：选择题

    （2014•泰安二模）以下四个命题中：

    ①为了了解800名学生对学校某项教改试验的意见，打算从中抽取一个容量为40的样本，考虑用系统抽样，则分段的间隔k为40．

    ②线性回归直线方程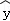=x+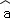恒过样本中心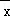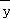（，），且至少过一个样本点；

    ③在某项测量中，测量结果ξ服从正态分布N（2，σ2）（σ＞0）．若ξ在（﹣∞，1）内取值的概率为0.1，则ξ在（2，3）内取值的概率为0.4；

    其中真命题的个数为（ ）

    A.0 B.1 C.2 D.3

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷（解析版） 题型：解答题

    （10分）（2004•北京）已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线y2=2px上，△ABC的重心与此抛物线的焦点F重合（如图）

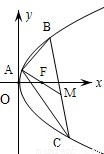
    （1）写出该抛物线的方程和焦点F的坐标；

    （2）求线段BC中点M的坐标

    （3）求BC所在直线的方程．

     

    查看答案和解析>>

    科目：高中数学 来源：2016届陕西省高一下学期期末考试数学试卷（解析版） 题型：解答题

    已知均为锐角，且，求的值。

     

    查看答案和解析>>

    同步练习册答案