
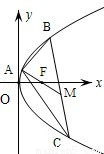
(10分)(2004•北京)已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合(如图)
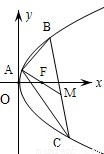
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标
(3)求BC所在直线的方程.
(1)抛物线方程为y2=32x,焦点F的坐标为(8,0)
(2)(11,﹣4)
(3)4x+y﹣40=0.
【解析】
试题分析:(1)由点A(2,8)在抛物线y2=2px上,将A点坐标代入,易求出参数p的值,代入即得抛物线的方程和焦点F的坐标;
(2)又由,△ABC的重心与此抛物线的焦点F重合,由重心坐标公式,易得线段BC中点M的坐标;
(3)设出过BC中点M的直线方程,根据联立方程、设而不求、余弦定理易构造关于直线斜率k的方程,解方程求出k值,进而可以得到直线的方程.
【解析】
(1)由点A(2,8)在抛物线y2=2px上,有82=2p•2解得p=16
所以抛物线方程为y2=32x,焦点F的坐标为(8,0)
(2)如图,由F(8,0)是△ABC的重心,M是BC的中点,AM是BC上的中线,由重心的性质可得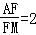 ;
;
设点M的坐标为(x0,y0),则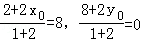 解得x0=11,y0=﹣4所以点M的坐标为(11,﹣4)
解得x0=11,y0=﹣4所以点M的坐标为(11,﹣4)
(3)由于线段BC的中点M不在x轴上,所以BC所在的直线不垂直于x轴.
设BC所成直线的方程为y+4=k(x﹣11)(k≠0)
由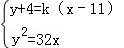 消x得ky2﹣32y﹣32(11k+4)=0
消x得ky2﹣32y﹣32(11k+4)=0
所以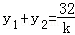 由(2)的结论得
由(2)的结论得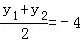 解得k=﹣4
解得k=﹣4
因此BC所在直线的方程为y+4=﹣4(x﹣11)即4x+y﹣40=0.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源:[同步]2014年人教A版选修四4-1第一讲1.1练习卷(解析版) 题型:选择题
如图,圆内接四边形ABCD中,AD∥BC,AC与BD交于点E,在图中全等三角形的对数为( )
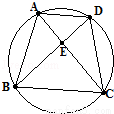
A.2对 B.3对 C.4对 D.5对
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.2练习卷(解析版) 题型:选择题
(2014•潍坊三模)为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到如下的2×2列联表.
| 喜爱打篮球 | 不喜爱打篮球 | 合计 |
男生 | 20 | 5 | 25 |
女生 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
则至少有( )的把握认为喜爱打篮球与性别有关.
A.95% B.99% C.99.5% D.99.9%
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•南昌三模)已知x,y的值如表所示:
x | 2 | 3 | 4 |
y | 5 | 4 | 6 |
如果y与x呈线性相关且回归直线方程为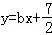 ,则b=( )
,则b=( )
A.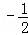 B.
B.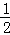 C.
C.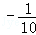 D.
D.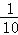
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:解答题
(12分)(2010•安徽)已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率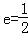 .
.
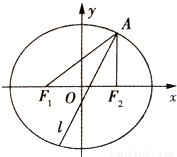
(1)求椭圆E的方程;
(2)求∠F1AF2的平分线所在直线l的方程;
(3)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)抛物线y2=10x的焦点到准线的距离是( )
A.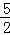 B.5 C.
B.5 C.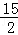 D.10
D.10
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)双曲线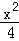 ﹣y2=1的渐近线方程是( )
﹣y2=1的渐近线方程是( )
A.x±2y=0 B.2x±y=0 C.4x±y=0 D.x±4y=0
查看答案和解析>>
科目:高中数学 来源:[同步]2014人教B版选修4-5 2.4最大值与最小值 优化数学模型(解析版) 题型:填空题
(2014•湖南二模)设x,y,z∈R,2x+2y+z+8=0,则(x﹣1)2+(y+2)2+(z﹣3)2之最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com