
(12分)(2010•安徽)已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率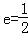 .
.
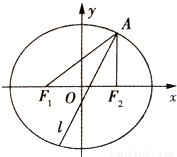
(1)求椭圆E的方程;
(2)求∠F1AF2的平分线所在直线l的方程;
(3)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.
(1) ;(2)2x﹣y﹣1=0;
;(2)2x﹣y﹣1=0;
(3)BC中点为(2,3)与A重合,不成立,所以不存在满足题设条件的相异的两点.
【解析】
试题分析:(1)设出椭圆方程,根据椭圆E经过点A(2,3),离心率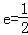 ,建立方程组,求得几何量,即可得到椭圆E的方程;
,建立方程组,求得几何量,即可得到椭圆E的方程;
(2)求得AF1方程、AF2方程,利用角平分线性质,即可求得∠F1AF2的平分线所在直线l的方程;
(3)假设存在B(x1,y1)C(x2,y2)两点关于直线l对称,设出直线BC方程代入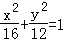 ,求得BC中点代入直线2x﹣y﹣1=0上,即可得到结论.
,求得BC中点代入直线2x﹣y﹣1=0上,即可得到结论.
【解析】
(1)设椭圆方程为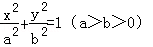
∵椭圆E经过点A(2,3),离心率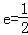
∴ ,
,
∴a2=16,b2=12
∴椭圆方程E为: ;
;
(2)F1(﹣2,0),F2(2,0),
∵A(2,3),
∴AF1方程为:3x﹣4y+6=0,AF2方程为:x=2
设角平分线上任意一点为P(x,y),则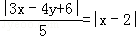 .
.
得2x﹣y﹣1=0或x+2y﹣8=0
∵斜率为正,∴直线方程为2x﹣y﹣1=0;
(3)假设存在B(x1,y1)C(x2,y2)两点关于直线l对称,∴
∴直线BC方程为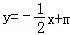 代入
代入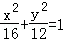 得x2﹣mx+m2﹣12=0,
得x2﹣mx+m2﹣12=0,
∴BC中点为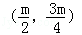
代入直线2x﹣y﹣1=0上,得m=4.
∴BC中点为(2,3)与A重合,不成立,所以不存在满足题设条件的相异的两点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年人教A版选修四4-1第一讲1.1练习卷(解析版) 题型:填空题
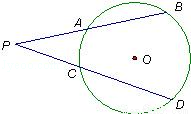
(2012•东莞市模拟)如图,P是圆O外一点,过P引圆O的两条割线PAB、PCD,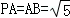 ,CD=3,则PC= .
,CD=3,则PC= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.2练习卷(解析版) 题型:选择题
(2014•黄山二模)某部门为了了解青年人喜欢户外运动是否与性别有关,运用2×2列联表进行独立性检验,经计算K2=7.069,则所得到的统计学结论为:有( )把握认为“喜欢户外运动与性别有关”.
附:(独立性检验临界值表)
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.636 | 7.879 | 10.828 |
A.0.1% B.1% C.99% D.99.9%
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•泰安二模)以下四个命题中:
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40.
②线性回归直线方程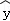 =
= x+
x+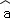 恒过样本中心(
恒过样本中心(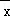 ,
,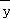 ),且至少过一个样本点;
),且至少过一个样本点;
③在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(﹣∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4;
其中真命题的个数为( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•咸阳一模)某产品在某零售摊位上的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:
x | 16 | 17 | 18 | 19 |
y | 50 | 34 | 41 | 31 |
由上表,可得回归直线方程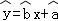 中的
中的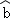 =﹣4,据此模型预计零售价定为15元时,每天的销售量为( )
=﹣4,据此模型预计零售价定为15元时,每天的销售量为( )
A.48个 B.49个 C.50个 D.51个
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:解答题
(10分)(2004•北京)已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合(如图)
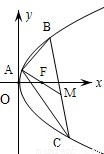
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标
(3)求BC所在直线的方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)已知点(x,y)在抛物线y2=4x上,则z=x2+ y2+3的最小值是( )
y2+3的最小值是( )
A.2 B.0 C.4 D.3
查看答案和解析>>
科目:高中数学 来源:[同步]2014人教B版选修4-5 2.4最大值与最小值 优化数学模型(解析版) 题型:填空题
设P是边长为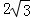 的正△ABC内的一点,x,y,z是P到三角形三边的距离,则
的正△ABC内的一点,x,y,z是P到三角形三边的距离,则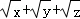 的最大值为 .
的最大值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com