
(2014•泰安二模)以下四个命题中:
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40.
②线性回归直线方程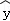 =
= x+
x+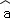 恒过样本中心(
恒过样本中心(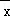 ,
,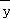 ),且至少过一个样本点;
),且至少过一个样本点;
③在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(﹣∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4;
其中真命题的个数为( )
A.0 B.1 C.2 D.3
B
【解析】
试题分析:①系统抽样时将整个的编号分段要确定分段的间隔,当总体个数除以样本容量是整数时,则间隔确定,当不是整数时,通过从总体中删除一些个体(用简单随机抽样的方法)使剩下的总体中个体的个数能被样本容量整除;
②根据样本点中心(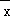 ,
,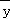 )点必在回归直线上,不一定过样本点,即可分析真假;
)点必在回归直线上,不一定过样本点,即可分析真假;
③根据ξ服从正态分布N(2,σ2)(σ>0),则正态分布图象的对称轴为x=2,
根据在(﹣∞,1)内取值的概率为0.1,进而得到随机变量ξ在(2,3)内取值的概率.
【解析】
①由题意知本题是一个系统抽样,
总体中个体数是800,样本容量是40,根据系统抽样的步骤,得到分段的间隔K=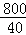 =20,故①是假命题;
=20,故①是假命题;
②线性回归直线方程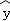 =
=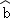 x+
x+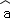 恒过样本中心(
恒过样本中心(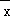 ,
,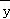 ),但不一定过样本点,故②是假命题;
),但不一定过样本点,故②是假命题;
③由于ξ服从正态分布N(2,σ2)(σ>0),则正态分布图象的对称轴为x=2,
故ξ在(﹣∞,2)内取值的概率为0.5,
又由ξ在(﹣∞,1)内取值的概率为0.1,则ξ在(1,2)内取值的概率为0.4
故ξ在(2,3)内取值的概率为0.4,故③是真命题;
故选:B


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:[同步]2014年人教A版选修四4-1第一讲1.2练习卷(解析版) 题型:选择题
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )

A.3和2 B.2和3 C.4和1 D.1和4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第四章4.2练习卷(解析版) 题型:选择题
(2007•淄博三模)下面的结构图,总经理的直接下属是( )
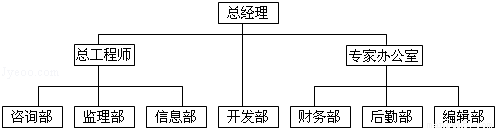
A.总工程师和专家办公室
B.开发部
C.总工程师、专家办公室和开发部
D.总工程师、专家办公室和所有七个部
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.2练习卷(解析版) 题型:选择题
(2014•潍坊三模)为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到如下的2×2列联表.
| 喜爱打篮球 | 不喜爱打篮球 | 合计 |
男生 | 20 | 5 | 25 |
女生 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
则至少有( )的把握认为喜爱打篮球与性别有关.
A.95% B.99% C.99.5% D.99.9%
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•西宁模拟)对具有线性相关关系的变量x和y,测得一组数据如下表:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
若已求得它们的回归直线方程的斜率为6.5,这条回归直线的方程为( )
A.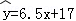 B.
B.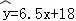 C.
C.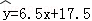 D.
D.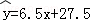
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•南昌三模)已知x,y的值如表所示:
x | 2 | 3 | 4 |
y | 5 | 4 | 6 |
如果y与x呈线性相关且回归直线方程为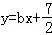 ,则b=( )
,则b=( )
A.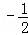 B.
B.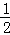 C.
C.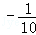 D.
D.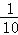
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:解答题
(12分)(2010•安徽)已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率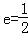 .
.
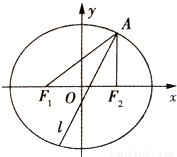
(1)求椭圆E的方程;
(2)求∠F1AF2的平分线所在直线l的方程;
(3)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)双曲线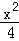 ﹣y2=1的渐近线方程是( )
﹣y2=1的渐近线方程是( )
A.x±2y=0 B.2x±y=0 C.4x±y=0 D.x±4y=0
查看答案和解析>>
科目:高中数学 来源:2016届陕西省高一下学期期末考试数学试卷(解析版) 题型:选择题
函数y=∣sinx∣+sin∣x∣的值域是( )
A.[-2,2] B.[-1,1] C.[0,1] D.[0,2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com