
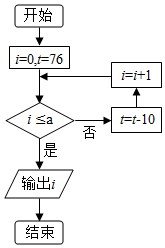
 执行如图所示的程序框图,若输出的i的值为8,则判断框内实数a的取值范围是[-4,6).(写成区间或集合的形式)
执行如图所示的程序框图,若输出的i的值为8,则判断框内实数a的取值范围是[-4,6).(写成区间或集合的形式) 分析 由循环变量的初值为0,步长为1,最后一次进入循环的终值为8,求出t的对应值,由此得出判断框内a的取值范围.
解答 解:由循环变量的初值为0,步长为1,
最后一次进入循环的终值为8,
第1次循环:t=76-10=66 i=0+1=1
第2次循环:t=66-10=56 i=1+1=2
第3次循环:t=56-10=46 i=2+1=3
第4次循环:t=46-10=36 i=3+1=4
…
第7次循环:t=16-10=6 i=6+1=7
第8次循环:t=6-10=-4 i=7+1=8
退出循环.此时t=-4≤a,不满足循环条件,输出i=8
则判断框内a的取值范围是-4≤a<6.
故答案为:[-4,6).
点评 本题考查了程序框图的应用问题,解题时应准确理解流程图的含义,是基础题目.


科目:高中数学 来源: 题型:解答题
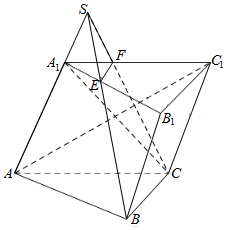 如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=BC=2,AC⊥BC,点S是侧棱AA1延长线上一点,EF是平面SBC与平面A1B1C1的交线.
如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=BC=2,AC⊥BC,点S是侧棱AA1延长线上一点,EF是平面SBC与平面A1B1C1的交线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 甲 | 12 | 13 | 14 | 15 | 16 |
| 乙 | 16 | 17 | 18 | 19 | a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com