
【题目】如图,已知双曲线C: ![]() ﹣y2=1(a>0)的右焦点为F,点A,B分别在C的两条渐近线AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).
﹣y2=1(a>0)的右焦点为F,点A,B分别在C的两条渐近线AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点). 
(1)求双曲线C的方程;
(2)过C上一点P(x0 , y0)(y0≠0)的直线l: ![]() ﹣y0y=1与直线AF相交于点M,与直线x=
﹣y0y=1与直线AF相交于点M,与直线x= ![]() 相交于点N.证明:当点P在C上移动时,
相交于点N.证明:当点P在C上移动时, ![]() 恒为定值,并求此定值.
恒为定值,并求此定值.
【答案】
(1)解:依题意知,A(c, ![]() ),设B(t,﹣
),设B(t,﹣ ![]() ),
),
∵AB⊥OB,BF∥OA,∴ ![]()
![]() =﹣1,
=﹣1, ![]() =
= ![]() ,
,
整理得:t= ![]() ,a=
,a= ![]() ,
,
∴双曲线C的方程为 ![]() ﹣y2=1
﹣y2=1
(2)证明:由(1)知A(2, ![]() ),l的方程为:
),l的方程为: ![]() ﹣y0y=1,
﹣y0y=1,
又F(2,0),直线l: ![]() ﹣y0y=1与直线AF相交于点M,与直线x=
﹣y0y=1与直线AF相交于点M,与直线x= ![]() 相交于点N.
相交于点N.
于是可得M(2, ![]() ),N(
),N( ![]() ,
, ![]() ),
),
∴ ![]() =
=  =
= ![]() =
= 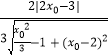 =
=  =
= ![]()
【解析】(1)依题意知,A(c, ![]() ),设B(t,﹣
),设B(t,﹣ ![]() ),利用AB⊥OB,BF∥OA,可求得a=
),利用AB⊥OB,BF∥OA,可求得a= ![]() ,从而可得双曲线C的方程;(2)易求A(2,
,从而可得双曲线C的方程;(2)易求A(2, ![]() ),l的方程为:
),l的方程为: ![]() ﹣y0y=1,直线l:
﹣y0y=1,直线l: ![]() ﹣y0y=1与直线AF相交于点M,与直线x=
﹣y0y=1与直线AF相交于点M,与直线x= ![]() 相交于点N,可求得M(2,
相交于点N,可求得M(2, ![]() ),N(
),N( ![]() ,
, ![]() ),于是化简
),于是化简 ![]() =
=  可得其值为
可得其值为 ![]() ,于是原结论得证.
,于是原结论得证.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点. 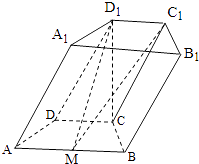
(1)求证:C1M∥平面A1ADD1;
(2)若CD1垂直于平面ABCD且CD1= ![]() ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点. 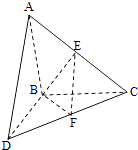
(1)求证:EF⊥BC;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某湿地公园内有一条河,现打算建一座桥将河两岸的路连接起来,剖面设计图纸如下:

其中,点![]() 为
为![]() 轴上关于原点对称的两点,曲线段
轴上关于原点对称的两点,曲线段![]() 是桥的主体,
是桥的主体,![]() 为桥顶,且曲线段
为桥顶,且曲线段![]() 在图纸上的图形对应函数的解析式为
在图纸上的图形对应函数的解析式为![]() ,曲线段
,曲线段![]() 均为开口向上的抛物线段,且
均为开口向上的抛物线段,且![]() 分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(
分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(![]() )的切线的斜率相等.
)的切线的斜率相等.
(1)求曲线段![]() 在图纸上对应函数的解析式,并写出定义域;
在图纸上对应函数的解析式,并写出定义域;
(2)车辆从![]() 经
经![]() 倒
倒![]() 爬坡,定义车辆上桥过程中某点
爬坡,定义车辆上桥过程中某点![]() 所需要的爬坡能力为:
所需要的爬坡能力为:![]() (该点
(该点![]() 与桥顶间的水平距离)
与桥顶间的水平距离)![]() (设计图纸上该点处的切线的斜率),其中
(设计图纸上该点处的切线的斜率),其中![]() 的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为
的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为![]() 米,
米,![]() 米,
米,![]() 米,又已知图纸上一个单位长度表示实际长度
米,又已知图纸上一个单位长度表示实际长度![]() 米,试问三种类型的观光车是否都可以顺利过桥?
米,试问三种类型的观光车是否都可以顺利过桥?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x+θ)+acos(x+2θ),其中a∈R,θ∈(﹣ ![]() ,
, ![]() )
)
(1)当a= ![]() ,θ=
,θ= ![]() 时,求f(x)在区间[0,π]上的最大值与最小值;
时,求f(x)在区间[0,π]上的最大值与最小值;
(2)若f( ![]() )=0,f(π)=1,求a,θ的值.
)=0,f(π)=1,求a,θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2+ex﹣ ![]() (x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
A.(﹣ ![]() )
)
B.( ![]() )
)
C.( ![]() )
)
D.( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程是![]() (θ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=-2cosθ.
(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=-2cosθ.
(1)写出C1的极坐标方程和C2的直角坐标方程;
(2)已知点M1、M2的极坐标分别是(1,π)、(2,![]() ),直线M1M2与曲线C2相交于P、Q两点,射线OP与曲线C1相交于点A,射线OQ与曲线C1相交于点B,求
),直线M1M2与曲线C2相交于P、Q两点,射线OP与曲线C1相交于点A,射线OQ与曲线C1相交于点B,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com