判断下列函数的奇偶性：
(1)f(x)＝x4＋x；
(2)f(x)＝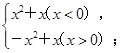
(3)f(x)＝lg(x＋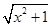
)．
阅读快车系列答案科目：高中数学 来源： 题型：解答题
设函数
的定义域为E，值域为F．
（1）若E={1，2}，判断实数λ=lg22+lg2lg5+lg5﹣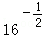
与集合F的关系；
（2）若E={1，2，a}，F={0，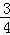
}，求实数a的值．
（3）若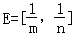
，F=[2﹣3m，2﹣3n]，求m，n的值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
求下列各题中的函数f(x)的解析式．
(1) 已知f(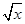
＋2)＝x＋4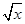，求f(x)；
(2) 已知f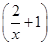
＝lgx，求f(x)；
(3) 已知函数y＝f(x)满足2f(x)＋f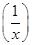
＝2x，x∈R且x≠0，求f(x)；
(4) 已知f(x)是二次函数，且满足f(0)＝1，f(x＋1)＝f(x)＋2x，求f(x)．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝lnx－ax2＋(2－a)x.
(1)讨论f(x)的单调性；
(2)设a>0，证明：当0<x<
时，f
>f
；
(3)若函数y＝f(x)的图象与x轴交于A、B两点，线段AB中点的横坐标为x0，证明：
＜0.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
设f(x)是定义在R上的奇函数，且对任意实数x，恒有f(x＋2)＝－f(x)，当x∈[0，2]时，f(x)＝2x－x2.
(1)求证：f(x)是周期函数；
(2)当x∈[2，4]时，求f(x)的解析式；
(3)计算f(0)＋f(1)＋f(2)＋…＋f(2014)的值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
（
为常数，且
）.
（1）当
时，求函数
的最小值（用表示）；
（2）是否存在不同的实数
使得
，
，并且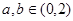
，若存在，求出实数的取值范围；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数
与听课时间
（单位：分钟）之间的关系满足如图所示的图像，当
时，图像是二次函数图像的一部分，其中顶点
，过点
；当
时，图像是线段
，其中
，根据专家研究，当注意力指数大于62时，学习效果最佳.
（1）试求
的函数关系式；
（2）教师在什么时段内安排内核心内容，能使得学生学习效果最佳？请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
在区间(0，＋∞)上的单调性．