
分析 (Ⅰ)由等差数列及正弦定理,得到B
(Ⅱ)化简f(x),由B的值,得到A的取值范围,由此得到f(A)的范围.
解答 解:(I)∵ccosA,bcosB,acosC成等差数列,
∴2bcosB=ccosA+acosC.
在△ABC中,由正弦定理a=2RsinA,b=2RsinB,c=2RsinC,R为△ABC外接圆的半径,
可得:2sinBcosB=sinCcosA+sinAcosC,
∴2sinBcosB=sin(A+C),
又A+C=π-B,
∴2sinBcosB=sin(π-B)=sinB,
∵$0<B<\frac{π}{2}$,∴sinB≠0,
∴$cosB=\frac{1}{2}$,∴$B=\frac{π}{3}$.
( II)$f(x)=\sqrt{3}sinxcosx-\frac{1}{2}cos2x=\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}cos2x$
=$sin(2x-\frac{π}{6})$.
∴$f(A)=sin(2A-\frac{π}{6})$,∵$B=\frac{π}{3}$,
∴$C=\frac{2π}{3}-A$,又$0<A<\frac{π}{2},0<C<\frac{π}{2}$,
∴$0<\frac{2π}{3}-A<\frac{π}{2}$,∴$\frac{π}{6}<A<\frac{π}{2}$,
∴$\frac{π}{6}<2A-\frac{π}{6}<\frac{5π}{6}$,
∴$\frac{1}{2}<sin(2A-\frac{π}{6})≤1$,
故f(A)的取值范围为$(\frac{1}{2},1]$.
点评 本题考查由等差数列及正弦定理、三角函数化简.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有且只有一条 | B. | 有两条 | C. | 有无穷多条 | D. | 必不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
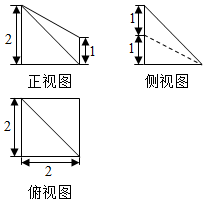
| A. | $\frac{5}{6}$ | B. | $\frac{10}{3}$ | C. | $\frac{7}{3}$ | D. | $\frac{17}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com