
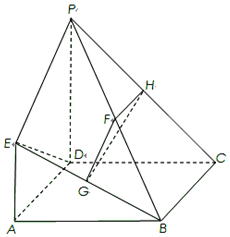
 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.分析 (1)证明PD⊥BD,PC⊥BC,根据直角三角形的中线特点得出F为外接球的球心,计算出球的半径代入面积公式计算即可;
(2)证明BC⊥平面ABE,FH∥BC即可得出FH⊥平面ABE,于是平面FGH⊥平面AEB;
(3)证明EF⊥PB,故只需FM⊥PB即可,利用相似三角形计算出PM.
解答 解:(1)连结FD,FC,
∵EA⊥平面ABCD,PD∥EA,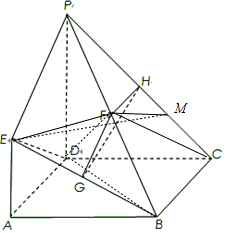
∴PD⊥平面ABCD,又BD?平面ABCD,
∴PD⊥BD,∵F是PB的中点,
∴DF=$\frac{1}{2}$PB,
同理可得FC=$\frac{1}{2}$PB,
∴F为棱锥P-BCD的外接球的球心.
∵AD=PD=2EA=2,
∴BD=2$\sqrt{2}$,PB=$\sqrt{P{D}^{2}+B{D}^{2}}$=2$\sqrt{3}$,
∴四棱锥P-BCD外接球的表面积为4π•($\frac{2\sqrt{3}}{2}$)2=12π.
(2)证明:∵EA⊥平面ABCD,BC?平面ABCD,
∴EA⊥CB.又CB⊥AB,AB∩AE=A,
∴CB⊥平面ABE.
∵F,H分别为线段PB,PC的中点,
∴FH∥BC.
∴FH⊥平面ABE.又FH?平面FGH,
∴平面FGH⊥平面ABE.
(3)在直角三角形AEB中,∵AE=1,AB=2,∴$BE=\sqrt{5}$.
在直角梯形EADP中,∵AE=1,AD=PD=2,∴$PE=\sqrt{5}$,
∴PE=BE.又F为PB的中点,
∴EF⊥PB.
假设在线段PC上存在一点M,使PB⊥平面EFM.
只需满足PB⊥FM即可,
∵PD⊥平面ABCD,BC?平面ABCD,
∴PD⊥CB,又CB⊥CD,PD∩CD=D,
∴CB⊥平面PCD,∵PC?平面PCD,
∴CB⊥PC.若PB⊥FM,则△PFM∽△PCB,∴$\frac{PM}{PB}=\frac{PF}{PC}$.
∵$PB=2\sqrt{3}$,$PF=\sqrt{3}$,$PC=2\sqrt{2}$,
∴$PM=\frac{{3\sqrt{2}}}{2}$.
∴线段PC上存在一点M,使PB⊥平面EFM,此时PM=$\frac{3\sqrt{2}}{2}$.
点评 本题考查了球与棱锥的位置关系,面面垂直的判定,线面垂直的判定,属于中档题.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:解答题
| 晕机 | 不晕机 | 总计 | |
| 男乘客 | |||
| 女乘客 | |||
| 总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | bf(lna)<af(lnb) | B. | bf(lna)=af(lnb) | ||
| C. | bf(lna)>af(lnb) | D. | bf(lna)与af(lnb)的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com