
| A. | bf(lna)<af(lnb) | B. | bf(lna)=af(lnb) | ||
| C. | bf(lna)>af(lnb) | D. | bf(lna)与af(lnb)的大小不确定 |
分析 由题意可知f'(x)-f(x)>0,构造辅助函数,求导,则g(x)在(-∞,+∞)上单调递增,由lna<lnb,则g(lna)<g(lnb),即可求得bf(lna)<af(lnb).
解答 解:由f'(x)>f(x),即f'(x)-f(x)>0,
设g(x)=$\frac{f(x)}{{e}^{x}}$,g(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$>0,
∴g(x)在(-∞,+∞)上单调递增,
由任意正数a,b,且a<b,则lna<lnb,
∴g(lna)<g(lnb),则$\frac{f(lna)}{a}$<$\frac{f(lnb)}{b}$,
∴bf(lna)<af(lnb),
故选A.
点评 本题考查导数的综合应用,考查利用导数研究函数的单调性,考查转化思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{9}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
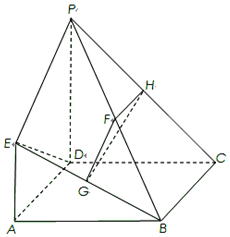 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{9}{16}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com