
���� ��1���������֪��a=0ʱ��x=1����������ɵ�1=3-k�����k�����ɵó�$x=3-\frac{2}{a+1}$��ÿ����Ʒ�����ۼ۸�Ϊ$15•\frac{8+16x}{x}$��Ԫ�����ɵ�2014�������y=x$��\frac{3}{2}•\frac{8+16x}{x}��$-��8+16x+a��=-$[\frac{16}{a+1}+��a+1��]+29$��a��0����
��2������һ�����û�������ʽ�����ʼ��ɵó���
�����������õ����о������ĵ����Լ�ֵ����ֵ�����ɵó���
��� �⣺��1���������֪��a=0ʱ��x=1�������
��1=3-k����k=2��
����$x=3-\frac{2}{a+1}$��ÿ����Ʒ�����ۼ۸�Ϊ$15•\frac{8+16x}{x}$��Ԫ��
��2014�������y=x$��\frac{3}{2}•\frac{8+16x}{x}��$-��8+16x+a��=4+8x-a=4+8$��3-\frac{2}{a+1}��$-a
=-$[\frac{16}{a+1}+��a+1��]+29$��a��0����
��2������һ����$a��0��\frac{16}{a+1}+��{a+1}����2\sqrt{16}=8$��
��y��-8+29=21�����ҽ���$\frac{16}{a+1}=��{a+1}��⇒a=3$����Ԫ��ʱ��ymax=21����Ԫ��
���Ե�������Ϊ3��Ԫʱ������������ֵ��21��Ԫ��
����������$y=x��{\frac{3}{2}��\frac{8+16x}{x}}��-��{8+16x+a}��$=4+8x-a
=$4+8��{3-\frac{2}{a+1}}��$-a=$��{-\frac{16}{a+1}}��$-a+28��y'=$\frac{16}{{{{��a+1��}^2}}}$-1��
��y'=0�����a=3������ԭ���������Ϊ21��Ԫ��
���� ���⿼���˺��������ʼ���Ӧ�á���������ʽ�����ʡ����õ����о������ĵ����Լ�ֵ����ֵ��������������������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | bf��lna����af��lnb�� | B�� | bf��lna��=af��lnb�� | ||
| C�� | bf��lna����af��lnb�� | D�� | bf��lna����af��lnb���Ĵ�С��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| ��ݴ���t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| �˾�������y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
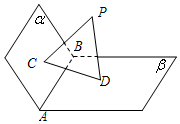 ��ͼ����֪ƽ������£��Ҧ��ɦ�=AB��PC�ͦ���PD�ͦ£�C��D�Ǵ��㣮
��ͼ����֪ƽ������£��Ҧ��ɦ�=AB��PC�ͦ���PD�ͦ£�C��D�Ǵ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{-\frac{1}{4}��0}��$ | B�� | $��{-\frac{1}{4}��0}]$ | C�� | $[{-\frac{1}{2}��1}]$ | D�� | $[{-\frac{1}{2}��1}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com