
分析 根据题意,若$\vec a∥\vec b$,由向量平行的坐标表示方法有1×y=2×(-2),解可得y的值,即可得$\overrightarrow{b}$的坐标,
(1)由向量数量积的坐标计算公式计算可得答案;
(2)由向量的坐标计算公式直接计算即可得答案.
解答 解:根据题意,已知$\vec a=({1,2}),\vec b=({-2,y})$,
若$\vec a∥\vec b$,则有1×y=2×(-2),即y=-4;
即$\overrightarrow{b}$=(-2,-4);
(1)$\overrightarrow{a}$•$\overrightarrow{b}$=1×(-2)+2×(-4)=-10;
(2)2$\overrightarrow{a}$-$\overrightarrow{b}$=(2,4)-(-2,-4)=(4,8).
点评 本题考查向量的坐标计算,关键要掌握向量的坐标计算以及数量积的计算公式.


科目:高中数学 来源: 题型:解答题
 20名学生某次数学成绩(单位:分)的频率分布直方图如图:
20名学生某次数学成绩(单位:分)的频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
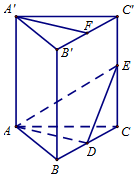 如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证:
如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{9}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com