
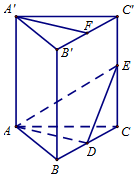
 如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证:
如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证:分析 (I)根据AD⊥BC,AD⊥BB′得出AD⊥平面BCC′B′,于是平面ADE⊥平面BCC'B';
(II)连结DF,证明四边形ADFA′是平行四边形得出A′F∥AD,于是A'F∥平面ADE.
解答 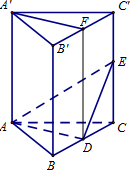 证明:(I)∵BB′⊥平面ABC,AD?平面ABC,
证明:(I)∵BB′⊥平面ABC,AD?平面ABC,
∴AD⊥BB′,
∵AD⊥BC,BB′∩BC=B,BB′?平面BCC′B′,BC?平面BCC′B′,
∴AD⊥平面BCC′B′,
又AD?平面ADE,
∴平面ADE⊥平面BCC'B'.
(II)连结DF,
∵AB=AC,AD⊥BC,
∴D是BC的中点,又F是B′C′的中点,
∴B′F$\stackrel{∥}{=}$BD,∴四边形BDFB′是平行四边形,
∴DF$\stackrel{∥}{=}$BB′,又BB′$\stackrel{∥}{=}$AA′,
∴DF$\stackrel{∥}{=}$AA′,∴四边形ADFA′是平行四边形,
∴A′F∥AD,
又A′F?平面ADE,AD?平面ADE,
∴A′F∥平面ADE.
点评 本题考查了面面垂直的判定,线面平行的判定,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | m∥β且l1∥α | B. | m∥l1且n∥l2 | C. | m∥β且n∥β | D. | m∥β且n∥l2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
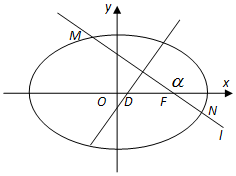 已知椭圆E的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),E上动点P到右焦点F距离的最大值为3,且离心率e=$\frac{1}{2}$.
已知椭圆E的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),E上动点P到右焦点F距离的最大值为3,且离心率e=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 晕机 | 不晕机 | 总计 | |
| 男乘客 | |||
| 女乘客 | |||
| 总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com